两生物种群竞争模型：LaTeX+Python

写在前面：本文是笔者数学建模课的作业，探讨了两生物种群竞争的常微分方程组模型的解的性质，展示了微分方程定性理论的基本思想。当然，本文最重要的目的，是展示LaTeX与Python的完美结合。（本文的图均由Python的Matplotlib模块生成；而文档则采用LaTeX编辑。）

问题提出 #

研究在同一个自然环境中生存的两个种群之间的竞争关系。假设两个种群独自在这个自然环境中生存时数量演变都服从Logistic规律，又假设当它们相互竞争时都会减慢对方数量的增长，增长速度的减小都与它们数量的乘积成正比。按照这样的假设建立的常微分方程模型为
$$\begin{equation}\label{eq:jingzhengfangcheng}\left\{\begin{aligned}\frac{dx_1}{dt}=r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2 \\
\frac{dx_2}{dt}=r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2\end{aligned}\right.\end{equation}$$
本文分别通过定量和定性两个角度来分析该方程的性质。

模型分析 #

在分析的过程中，我们所采用的模型参数是
$$\begin{equation}\label{eq:fangchengcanshu}\left\{\begin{aligned}
&r_1 = 0.1,\frac{1}{N_1}=0.002,a_1=0.0001\\
&r_2=0.3,\frac{1}{N_2}=0.003,a_2=0.0002\\
&x_1(0)=100,x_2(0)=150
\end{aligned}\right.\end{equation}$$

这些参数表明，$x_1$是一个增长相对缓慢的物种，但是种内竞争较小，而且不容易受到$x_2$物种的影响，因此，长远来看，$x_1$物种将在该自然环境中占优；相比之下，$x_2$物种的增长速度较快，但是种内竞争较大，而且容易受到$x_1$物种的影响，因此在长期的竞争中，$x_2$物种将处于稍弱的地位。下面的数值求解结果支持了这一推测。

数值解

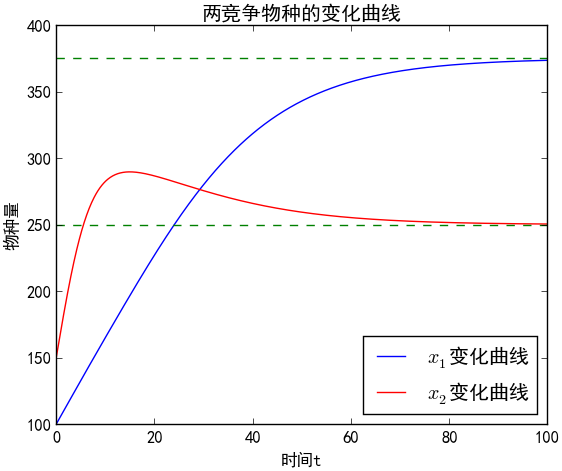
结合$(1)$和$(2)$，我们利用Python对该模型进行了数值求解。得到结果如下图

数值解表明，$x_2$物种开始增长较快，达到最大值后开始缓慢下降，最后稳定在250；而$x_1$则保持相对较慢的增长速度，直到平衡点375。下面我们分析$(1)$的平衡点的性质。

平衡点

方程$(1)$的平衡点的决定方程为
$$\begin{equation}\label{eq:pinghengdianfangcheng}\left\{\begin{aligned}r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2=0 \\
r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2=0\end{aligned}\right.\end{equation}$$

该方程有4个解
$$\begin{equation}\label{eq:pinghengdian} \left\{\begin{aligned}&x_1 =0\\&x_2 =0\end{aligned}\right., \quad \left\{\begin{aligned}&x_1 =0\\&x_2 =N_2\end{aligned}\right.,\quad \left\{\begin{aligned}&x_1 = N_1\\&x_2 =0\end{aligned}\right.,\quad \left\{\begin{aligned}&x_1 = \frac{N_1 r_2 (a_1 N_2 -r_1 )}{a_1 a_2 N_1 N_2-r_1 r_2}\\&x_2 =\frac{N_2 r_1 (a_2 N_1- r_2)}{a_1 a_2 N_1 N_2-r_1 r_2} \end{aligned}\right.\end{equation}$$

其中前三个平衡点是平凡的平衡点，最后一个是非平凡的。可以发现，当参数为$(2)$时，方程$(1)$最终收敛于第四个平衡点，这说明第四个平衡点具有较强的稳定性。下面我们通过方程的方向场图和相图来分析平衡点的稳定性和方程的整体性质。

方向场

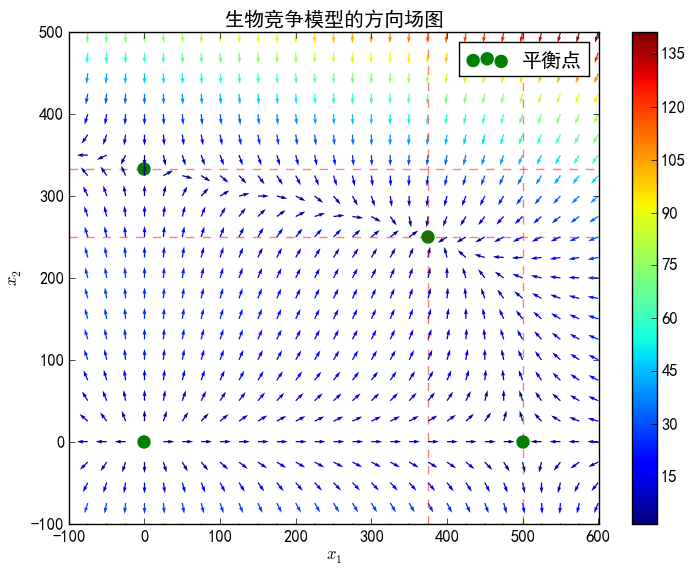
下图是我们作出的关于$(1)$和$(2)$的方向场图，其中平衡点已经用绿色点标出。箭头颜色的深浅，代表着在在该点处变化的快慢。

从方向场图中可以比较地容易判断四个平衡点的稳定性。

第一个平衡点，即左下方的$(0,0)$，也就是两物种数量都是0的情况，属于不稳定平衡点，所有的箭头都朝着远离该平衡点的方向，这意味着平衡点附近微小的扰动，将会导致最终远离平衡点。也就是说，只要有小量物种在这里生存，最终都将繁衍起来，达到另外的平衡点。

第二个平衡点，即左上方的$(0,N_2)$，也就是只有$x_2$物种的情形，属于不稳定平衡点（鞍点），只有过该点的竖直线上的箭头指向该点，其余所有的箭头都朝着远离该平衡点的方向，这说明该平衡点稳定性比$(0,0)$要强，但是同样不稳定，只要有小量$x_1$物种的存在，都会由于竞争而远离目前的平衡点。

第三个平衡点，即右下方的$(N_1,0)$，也就是只有$x_1$物种的情形，属于不稳定平衡点（鞍点），只有过该点的水平线上的箭头指向该点，其余所有的箭头都朝着远离该平衡点的方向，这说明该平衡点稳定性比$(0,0)$要强，但是同样不稳定，只要有小量$x_2$物种的存在，都会由于竞争而远离目前的平衡点。

第四个平衡点，即右上方的$\left(\frac{N_1 r_2 (a_1 N_2 -r_1 )}{a_1 a_2 N_1 N_2-r_1 r_2},\frac{N_2 r_1 (a_2 N_1- r_2)}{a_1 a_2 N_1 N_2-r_1 r_2}\right)$ ，两个物种都存在且达到平衡，属于稳定平衡点，该点附近所有的箭头指向该点，这说明即使偏离该平衡点，最终还是会回到该平衡点。

相轨线

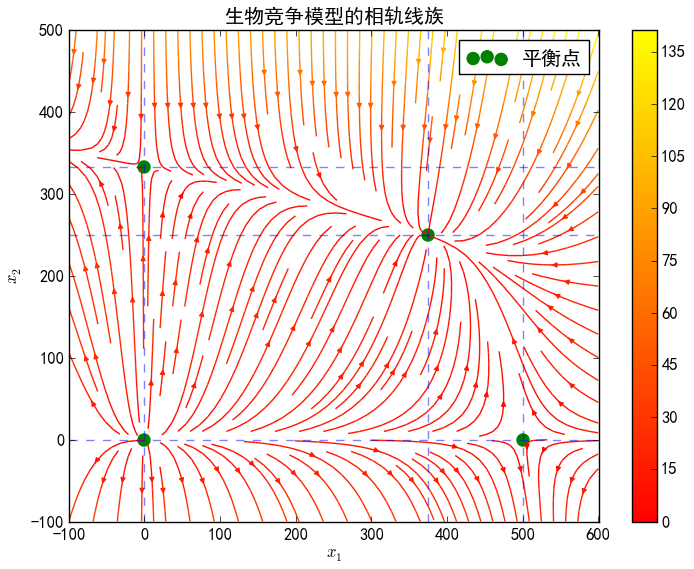
从下面的相轨线族图中，可以更清楚地看到平衡点附近的流动情况。可以看到，几乎第一象限内（第一象限内对应于有实际意义的解）的流线都汇集到第四个平衡点，说明第四个平衡点具有非常强的稳定性，该平衡点是任意初始条件的最终稳定点。

可以发现，相轨线族图中，并没有封闭的相轨线，因此，方程并不存在周期振荡的解。

代码列表 #

以下代码需要Python3+Numpy+Scipy+Matplotlib的运行环境。

数值解

from scipy.integrate import odeint
import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #这两句用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False

t = np.arange(0,100,0.1)

def deriv(w,t,a,b,c,d,e,f): 
    x,y = w
    return np.array([ a*(1-b*x)*x-c*y*x, d*(1-e*y)*y-f*x*y])

p=[0.1, 0.002, 0.0001, 0.3, 0.003, 0.0002, 100, 150]

a,b,c,d,e,f,x0,y0=p
yinit = np.array([x0,y0]) # 初值
yyy = odeint(deriv,yinit,t,args=(a,b,c,d,e,f))

plt.figure(figsize=(7,5))
plt.plot(t,yyy[:,0],"b-",label="$x_1$变化曲线")
plt.plot(t,yyy[:,1],"r-",label="$x_2$变化曲线")
plt.plot([0,100],[250,250],"g--")
plt.plot([0,100],[375,375],"g--")
plt.xlabel(u'时间t')
plt.ylabel(u'物种量')
plt.title(u'两竞争物种的变化曲线')
plt.legend(loc=4)
plt.show()

方向场

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #这两句用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False

p=[0.1, 0.002, 0.0001, 0.3, 0.003, 0.0002]
x0=np.array([0,0,1/0.002,375])
y0=np.array([0,1/0.003,0,250])
a,b,c,d,e,f=p
x,y = np.mgrid[-100:601:25,-100:501:25]
#x,y = np.mgrid[300:401:5,200:300:5]
s = a*(1-b*x)*x-c*y*x
t = d*(1-e*y)*y-f*x*y
r = np.sqrt(s**2+t**2)
plt.figure(figsize=(7*1.2,6))
plt.plot([-100,600],[1/0.003,1/0.003], 'r--',alpha=0.5)
plt.plot([-100,600],[250,250], 'r--',alpha=0.5)
plt.plot([500,500],[-100,500], 'r--',alpha=0.5)
plt.plot([375,375],[-100,500], 'r--',alpha=0.5)
plt.scatter(x0,y0, s=75,color ='green',label='平衡点')
plt.quiver(x,y,s/r,t/r,r)
plt.colorbar()
plt.xlim(-100,601)
plt.ylim(-100,501)
plt.xlabel(u'$x_1$')
plt.ylabel(u'$x_2$')
plt.title(u'生物竞争模型的方向场图')
plt.legend()
plt.show()

相图

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #这两句用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False

x0=np.array([0,0,1/0.002,375])
y0=np.array([0,1/0.003,0,250])
p=[0.1, 0.002, 0.0001, 0.3, 0.003, 0.0002]
a,b,c,d,e,f=p
y, x = np.mgrid[-100:501:5,-100:601:5]
s = a*(1-b*x)*x-c*y*x
t = d*(1-e*y)*y-f*x*y
r = np.sqrt(s**2+t**2)
plt.figure(figsize=(7*1.2,6))
plt.plot([-100,600],[1/0.003,1/0.003], 'b--',alpha=0.5)
plt.plot([-100,600],[250,250], 'b--',alpha=0.5)
plt.plot([500,500],[-100,500], 'b--',alpha=0.5)
plt.plot([375,375],[-100,500], 'b--',alpha=0.5)
plt.plot([0,0],[-100,500], 'b--',alpha=0.5)
plt.plot([-100,600],[0,0], 'b--',alpha=0.5)
plt.scatter(x0,y0, s=75,color ='green',label='平衡点')
plt.streamplot(x, y, s, t, color=r, density=1.5,linewidth=1, cmap=plt.cm.autumn)
plt.colorbar()
plt.xlim(-100,601)
plt.ylim(-100,501)
plt.xlabel(u'$x_1$')
plt.ylabel(u'$x_2$')
plt.title(u'生物竞争模型的相轨线族')
plt.legend()
plt.show()

转载到请包括本文地址：https://spaces.ac.cn/archives/3120

更详细的转载事宜请参考：《科学空间FAQ》