《自然极值》系列——1.前言
By 苏剑林 | 2010-11-27 | 62186位读者 | Kimi 引用附:期中考过后,课程紧了,自由时间少了,因此科学空间的更新也放缓了。不过BoJone也会尽量地更新一些内容,和大家一同分享学习的乐趣。
上一周和这一周的时间里,BoJone将自己学习物理和极值的一些内容进行了总结和整合,写成了《自然极值》一文。因此从今天起,到十二月的大多数时间里,科学空间将和大家讲述并讨论关于“极值”的问题,希望读者会喜欢这部分内容。当然,我不是专业的研究人员,更不是经验丰富的物理和数学教师,甚至可以说是一个“乳臭未干的小子”,因此,错误在所难免,只希望同好不吝指出,更希冀能够起到我抛出的这一块“砖”能够引出美妙的“玉”。
意犹未尽——继续光学曲线
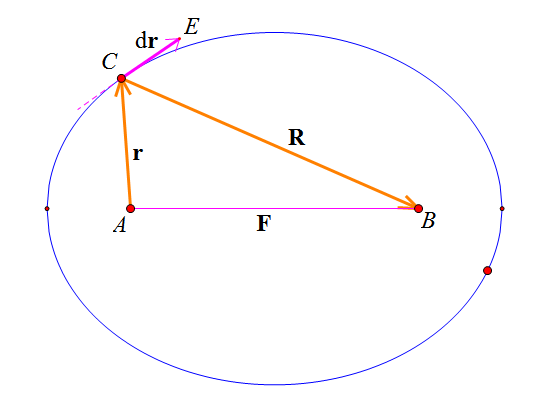
By 苏剑林 | 2010-11-13 | 72437位读者 | Kimi 引用为什么是抛物线?——聚光面研究
By 苏剑林 | 2010-11-07 | 110034位读者 | Kimi 引用警察捉贼,追牛问题,导弹跟踪
By 苏剑林 | 2010-11-06 | 70450位读者 | Kimi 引用王二小的牛跑了,当他发现时,牛在他正南方300米。且一直向正西方向匀速的跑,王二小立即追牛,他不是朝着一个固定的方向,而是每时每刻都朝着牛的方向跑,且速度是牛速度的4/3倍。当他追上牛时王二小共跑了多远?
问题分析
咋看起来,追牛和导弹是风牛马不相及的两件事:一个是生活小事,一个是物理问题,怎么能够扯到一块呢?
回想一下平时警察抓小偷的过程。警察不是物理学家,不会也可不能先去研究小偷的逃走路线函数,然后设计最小追赶时间的路程吧?那么,在不能预知小偷逃跑路线的前提下,警察要怎样捉小偷呢?很简单,盯死他!是的,只要你以更快的速度,一直朝着他跑,总能够追到的。继续联想下:要想用导弹跟踪摧毁一首敌舰,不也是只能够采用这种方式吗?回看文章开始的“追牛问题”,本质上不是一样的吗?以下是上海交大提出的导弹跟踪问题:
这个星期对微分方程的认识
By 苏剑林 | 2010-11-06 | 44530位读者 | Kimi 引用这个星期研究了两道微分方程问题:“导弹跟踪”以及“太阳炉”问题。从中我加深了对微分方程的理解,也熟悉了微分方程的相关运算。仅此记录,权当抛砖引玉。
一、微分方程的本质
很多读者都知道,自从牛顿和莱布尼兹发明微积分之后,微积分就迅速地渗透到了几乎所有的学科,后来发展出许多出色的分支,如变分、微分方程等。众所周知,微分方程是解决很多重要问题的工具。不知道各位读者对微分及微分方程的认识如何?其实对于常微分方程而言,它的本质和我们已经学习过的代数方程一样,只不过相互之间的对应运算关系除了常规的加减乘除幂等之外,还多了两个相互关系:微分和积分。例如对于一阶微分方程$\dot{y}=f(x,y)$,也许大家都认为它是一个二元方程,其实不然,这是一个“四个未知数、三道方程”所组成的方程组,我们可以将它写成
$$dy=f(x,y)dx,y=\int dy,x=\int dx$$







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 ![闭区间[a,b]上的连续函数?(x),其最大值为红色点,最小值为蓝色点](/usr/uploads/2010/11/3941873990.png)




最近评论