【理解黎曼几何】8. 处处皆几何 (力学几何化)
By 苏剑林 | 2016-11-02 | 53769位读者 | 引用黎曼几何在广义相对论中的体现和应用,虽然不能说家喻户晓,但想必大部分读者都有所听闻。一谈到黎曼几何在物理学中的应用,估计大家的第一反应就是广义相对论。常见的观点是,广义相对论的发现大大推动了黎曼几何的发展。诚然,这是事实,然而,大多数人不知道的事,哪怕经典的牛顿力学中,也有黎曼几何的身影。
本文要谈及的内容,就是如何将力学几何化,从而使用黎曼几何的概念来描述它们。整个过程事实上是提供了一种框架,它可以将不少其他领域的理论纳入到黎曼几何体系中。
黎曼几何的出发点就是黎曼度量,通过黎曼度量可以通过变分得到测地线。从这个意义上来看,黎曼度量提供了一个变分原理。那反过来,一个变分原理,能不能提供一个黎曼度量呢?众所周知,不少学科的基础原理都可以归结为一个极值原理,而有了极值原理就不难导出变分原理(泛函极值),如物理中就有最小作用量原理、最小势能原理,概率论中有最大熵原理,等等。如果有一个将变分原理导出黎曼度量的方法,那么就可以用几何的方式来描述它。幸运的是,对于二次型的变分原理,是可以做到的。
调侃:万有引力与爱因斯坦的理论
By 苏剑林 | 2016-05-18 | 44526位读者 | 引用我不是研究引力的,也没有很好地学习过引力。在理论物理方面,我学习经典力学和量子力学比学习广义相对论要多得多。因此,本来我是不应该谈引力的,以免误人子弟。不过,在一次坐车的途中,司机的刹车和加速让我联想到了一些跟引力有关的东西,自我感觉比较有趣,所以发给大家分享一下,也请大家指正。
等效原理
引力,准确来说应该是“万有引力”。所谓“万有”,有两个含义:1、所有物体都能够产生引力;2、所有物体都被引力影响。一个力居然是“万有”的,这让爱因斯坦感觉到非常奇怪,这也是四种基本力之中,引力跟其他力区别最明显的地方。相比之下,电磁相互作用力就只能存在于有“电”的地方,弱相互作用只存在于费米子,等等。
除了引力之外,我们平时还遇到过什么“万有”的力吗?貌似没有。但是我们想象一下,当你坐在一辆长途大巴匀速前进时,突然司机来了一个急刹车,在刹车的那一瞬间,所有人都往前倾了,不仅如此,可能你的行李箱、你的随身物品都往前移的,事实上,车上所有东西都受到了一个往前的力!对于那辆车上的人和物来说,刹车的那一瞬间,就存在着一个“万有”的力!
力的无穷分解与格林函数法
By 苏剑林 | 2014-11-24 | 32014位读者 | 引用我小时候一直有个疑问:
直升机上的螺旋桨能不能用来挡雨?
一般的螺旋桨是若干个“条状”物通过旋转对称而形成的,也就是说,它并非一个面,按常理来说,它是没办法用来挡雨的。但是,如果在高速旋转的情况下,甚至假设旋转速度可以任意大,那么我们任意时刻都没有办法穿过它了,这种情况下,它似乎与一个实在的面无异?
力的无穷分解
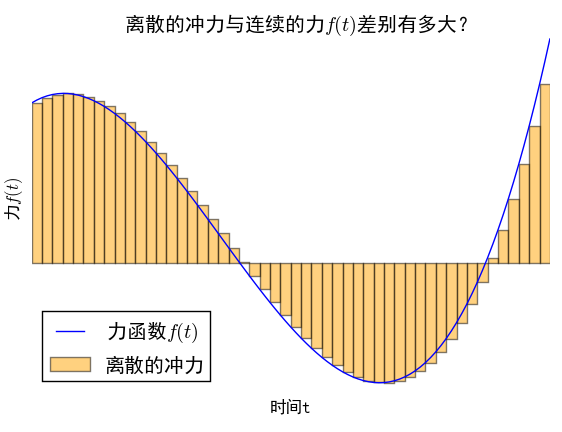
当然,以上只是笔者小时候的一个“异想天开”的念头,读者不必较真。不过,这个疑问跟本文有什么联系呢?我们在研究振动问题之时,通常会遇到在变力的作用下的受迫振动问题,已知变力是时间的函数,比如$f(t)$,然而,虽然知道$f(t)$的具体形式,但是由于$f$的非线性性,加上外力之后的运动,不一定容易求解。然而,如果可以将一个变化的力分段为无数个无穷小时间内的恒力(冲力),那么我们就可以分段讨论我们要研究的运动,而通常来说,恒力的问题会比变力容易。将一个变力离散化,然后再取极限,那么是不是跟原来在变力下的运动是一样的呢?这跟文章开头的疑问有着类似的思想——离线的极限,跟连续本身,是不是等价的?而让人惊喜的是,在通常的物理系统中,将力分段为无数个小区间内的恒力的做法,能够导致正确的答案,而且,这恰好是线性常微分方程的格林函数法。下面我们来分析这一做法。
最近的很多篇文章都是数论内容,属于纯数学的范畴了,对于很多只爱好物理或应用数学的读者可能会看得头晕了。今天我们来谈些不那么抽象的东西,我们来谈谈风筝,并来分析一下风筝的飞行力学。
爱情就像放风筝,线不能来得太紧,也不能拉得太松,你只会给对方飞翔的空间,他/她始终会回到你身边,因为有一条线系着双方。
风筝,在我们这个地方叫做纸鸢,相信大家童年时一定会放过。笔者小时候放风筝时,已经是小学五年级之前的事了。这个暑假突然童心一起,凭着小时候的回忆,简单做了个风筝来玩,居然真的飞起来了!兴奋之余,与大家分享一下。如今再来放风筝,真心感觉到放风筝也有很多技巧,让风筝飞,还不是件容易的事情呢,真可谓人生处处皆学问呀。上面关于风筝的比喻,正是放风筝的真实写照吧。
风筝可以说是人类摆脱地球重力的最原始尝试吧,跟发射宇宙飞船的火箭不同,风筝是借助风力来抵抗重力,严格来讲,即便是现在的飞机,也离不开这个原理(我们最后会谈到)。简单来讲,风筝就是用轻的支架撑开一个轻盈的平面,然后系上一个线圈。我们简单做一个风筝,只需要一张报纸,两条竹篾和一点透明胶,十分钟内就可以完成一个。当然,现在已经有各种各样的好看的风筝,甚至还有龙形的风筝,但是,自己动手简单做一个风筝,还是相当好玩的。
风筝自然是借助风力飞起来的,可是为什么风筝得用绳子牵着才能飞得更高、绳断了反而掉下来?风大多时,才适合放风筝?飞机又是怎么飞起来的?下面我们试着分析这些问题。
一本对称闯物理:相对论力学(二)
By 苏剑林 | 2014-03-25 | 16631位读者 | 引用从这个系列的第一篇文章到本文,已经隔了好多天。其实本文的内容是跟第一篇的内容同时完成的,为什么这么久才更新呢?原因有二,其一是随着春天的到来人也开始懒起来了,颓废呀~;其二,我在思考着规范变换的问题。按照朗道《场论》的逻辑,发展完质点力学理论后,下一步就是发展场论,诸如电磁场、引力场等。但是场论中有个让我比较困惑的东西,即场论存在着“规范不变性”。按照一般观点,我们是将规范不变性看作是电磁场方程的一个结果,即推导出电磁场的方程后,“发现”它具有规范不变性。但是如果用本文的方法,即假定场有这种对称性,然后就可以构建出场方程了。可是,为什么场存在着规范不变性,我还未能思考清楚。据我阅读到的资料来看,这个不变性似乎跟广义不变性有关(电磁场也是,这似乎说明即使在平直时空的电磁场理论中也暗示了广义不变性?)。还有,似乎这个不变性需要在量子场论中才能得到比较满意的解释,可是这样的话,就离我还很远了。
好吧,我们还是先回到相对论力学的推导中。
“无”中生有
上一篇文章我们已经构建了相对论力学的无穷小生成元,并进行了延拓。我已经说过,仅需要无穷小的变换形式,就可以构建出完成的相对论力学定律出来(当然这需要一些比较“显然”的假设)。这是个几乎从“无”到有的过程,也是本文标题的含义所在。另一方面,这种从局部到整体的可能性,也给我们带来一些启示:假如方法是普适的,那么可以由此构造出我们需要的物理定律来,包括电磁场、引力场方程等。(当然,我离这个目标还有点远。)
一本对称闯物理:相对论力学(一)
By 苏剑林 | 2014-03-19 | 27847位读者 | 引用简单说说
笔者最近陶醉于从李对称的角度来理解力学和场论,并且计算得到一些比较有趣的结果,遂想在此与大家分享。我发现,仅仅需要一个描述对称的无穷小生成元和一些最基本的假设,几乎就可以完成地推导出整个相对论力学来,甚至推导出整个(经典)场论理论来。这确实是不可思议的,我现在能基本体会到当年徐一鸿大师写的《可畏的对称》的含义了。对称的威力如此之大,以至于我们真的不得不敬畏它。而在构思本文题目的时候,我也曾想到过用“可畏的对称”为题,但不免有抄袭和老套之嫌。后来想到曾有一部漫画叫《一本漫画闯天涯》,遂将“漫画”改成“对称”,“天涯”改成“物理”,似乎也能表达我对“对称”的感觉。
对称就是在某种变换下保持不变的性质,比如狭义相对论要求所有物理定律在所有惯性系中保持不变,这相对于要求描述物理定律的方程在匀速运动的坐标变换下保持不变,结合光速不变的要求,我们就可以推导出洛伦兹变换,从而完成地描述了狭义相对论里边的对称。然而,并不是任何时候都可以想推导洛伦兹变换那样,能够把一个完整的变换推导出来的。幸好,李对称的不需要完整的对称描述,它只需要“无穷小变换”(意味着我们可以忽略掉高阶项),对应地产生一个“无穷小生成元”,用这个无穷小生成元,就足以完整构建出我们所需要的物理来。这种“无穷小”决定“广泛”、“局部”决定“全局”的奇妙至今仍让我觉得不可思议。(关于李对称、无穷小生成元的基本概念,不妨先阅读:《求解微分方程的李对称方法》)
Mathieu方程
在文章《有质动力:倒立单摆的稳定性》中,我们分析了通过高频低幅振荡来使得倒立单摆稳定的可能性,并且得出了运动方程
$$l\ddot{\theta}+[h_0 \omega^2 \cos(\omega t)-g]\sin\theta=0$$
由此对单摆频率的下限提出了要求$\omega \gg \sqrt{\frac{g}{h_0}}$。然而,那个下限只不过是必要的,却不是充分的。如果要完整地分析该单摆的运动方程,最理想的方法当然是写出上述常微分方程的解析解。不过很遗憾,我们并没有办法做到这一点。我们只能够采取各种近似方法来求解。近似方法一般指数值计算方法,然后笔者偏爱的是解析方法,也就是说,即使是近似解,也希望能够求出近似的解析解。
一维弹簧的运动(下)
By 苏剑林 | 2014-03-13 | 24416位读者 | 引用在上一篇文章中,我们得到了一维弹簧运动的方程
$$m\frac{\partial^2 X}{\partial t^2}=k\frac{\partial^2 X}{\partial \xi^2}$$
并且得到了通解
$$X=F(u)+H(v)=F(\xi+\beta t)+H(\xi-\beta t)$$
或者
$$X(\xi,t)=\frac{1}{2}\left[X_0(\xi+\beta t)+X_0(\xi-\beta t)\right]+\frac{1}{2\beta}\int_{\xi-\beta t}^{\xi+\beta t} X_1 (s)ds$$
在文章的末尾,提到过这个解是有些问题的。现在让我们来详细分析它。











最近评论