Monarch矩阵:计算高效的稀疏型矩阵分解
By 苏剑林 | 2024-07-24 | 1867位读者 | 引用在矩阵压缩这个问题上,我们通常有两个策略可以选择,分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸,而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的,那么相应地寻找矩阵稀疏近似的算法又是什么呢?
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》,它为上述问题给出了一个答案——“Monarch矩阵”,这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵,同时具备计算高效且表达能力强的特点,论文还讨论了如何求一般矩阵的Monarch近似,以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。
值得指出的是,该论文的作者也正是著名的Flash Attention的作者Tri Dao,其工作几乎都在致力于改进LLM的性能,这篇Monarch也是他主页上特意展示的几篇论文之一,单从这一点看就非常值得学习一番。
【生活杂记】用电饭锅来煮米汤
By 苏剑林 | 2024-07-17 | 2778位读者 | 引用对齐全量微调!这是我看过最精彩的LoRA改进(一)
By 苏剑林 | 2024-07-12 | 11250位读者 | 引用众所周知,LoRA是一种常见的参数高效的微调方法,我们在《梯度视角下的LoRA:简介、分析、猜测及推广》做过简单介绍。LoRA利用低秩分解来降低微调参数量,节省微调显存,同时训练好的权重可以合并到原始权重上,推理架构不需要作出改变,是一种训练和推理都比较友好的微调方案。此外,我们在《配置不同的学习率,LoRA还能再涨一点?》还讨论过LoRA的不对称性,指出给$A,B$设置不同的学习率能取得更好的效果,该结论被称为“LoRA+”。
为了进一步提升效果,研究人员还提出了不少其他LoRA变体,如AdaLoRA、rsLoRA、DoRA、PiSSA等,这些改动都有一定道理,但没有特别让人深刻的地方觉。然而,前两天的《LoRA-GA: Low-Rank Adaptation with Gradient Approximation》,却让笔者眼前一亮,仅扫了摘要就有种必然有效的感觉,仔细阅读后更觉得它是至今最精彩的LoRA改进。
究竟怎么个精彩法?LoRA-GA的实际含金量如何?我们一起来学习一下。
“闭门造车”之多模态思路浅谈(二):自回归
By 苏剑林 | 2024-07-08 | 9511位读者 | 引用这篇文章我们继续来闭门造车,分享一下笔者最近对多模态学习的一些新理解。
在前文《“闭门造车”之多模态思路浅谈(一):无损》中,我们强调了无损输入对于理想的多模型模态的重要性。如果这个观点成立,那么当前基于VQ-VAE、VQ-GAN等将图像离散化的主流思路就存在能力瓶颈,因为只需要简单计算一下信息熵就可以表明离散化必然会有严重的信息损失,所以更有前景或者说更长远的方案应该是输入连续型特征,比如直接将图像的原始像素特征Patchify后输入到模型中。
然而,连续型输入对于图像理解自然简单,但对图像生成来说则引入了额外的困难,因为非离散化无法直接套用文本的自回归框架,多少都要加入一些新内容如扩散,这就引出了本文的主题——如何进行多模态的自回归学习与生成。当然,非离散化只是表面的困难,更艰巨的部份还在后头...
无损含义
首先我们再来明确一下无损的含义。无损并不是指整个计算过程中一丁点损失都不能有,这不现实,也不符合我们所理解的深度学习的要义——在2015年的文章《闲聊:神经网络与深度学习》我们就提到过,深度学习成功的关键是信息损失。所以,这里无损的含义很简单,单纯是希望作为模型的输入来说尽可能无损。
重温SSM(四):有理生成函数的新视角
By 苏剑林 | 2024-06-27 | 7489位读者 | 引用在前三篇文章中,我们较为详细地讨论了HiPPO和S4的大部分数学细节。那么,对于接下来的第四篇文章,大家预期我们会讨论什么工作呢?S5、Mamba乃至Mamba2?都不是。本系列文章主要关心SSM的数学基础,旨在了解SSM的同时也补充自己的数学能力。而在上一篇文章我们简单提过S5和Mamba,S5是S4的简化版,相比S4基本上没有引入新的数学技巧,而Mamba系列虽然表现优异,但它已经将$A$简化为对角矩阵,所用到的数学技巧就更少了,它更多的是体现了工程方面的能力。
这篇文章我们来学习一篇暂时还声名不显的新工作《State-Free Inference of State-Space Models: The Transfer Function Approach》(简称RFT),它提出了一个新方案,将SSM的训练、推理乃至参数化,都彻底转到了生成函数空间中,为SSM的理解和应用开辟了新的视角
基础回顾
首先我们简单回顾一下上一篇文章关于S4的探讨结果。S4基于如下线性RNN
\begin{equation}\begin{aligned}
x_{k+1} =&\, \bar{A} x_k + \bar{B} u_k \\
y_{k+1} =&\, \bar{C}^* x_{k+1} \\
\end{aligned}\label{eq:linear}\end{equation}
重温SSM(三):HiPPO的高效计算(S4)
By 苏剑林 | 2024-06-20 | 9568位读者 | 引用前面我们用两篇文章《重温SSM(一):线性系统和HiPPO矩阵》和《重温SSM(二):HiPPO的一些遗留问题》介绍了HiPPO的思想和推导——通过正交函数基对持续更新的函数进行实时逼近,其拟合系数的动力学正好可以表示为一个线性ODE系统,并且对于特定的基底以及逼近方式,我们可以将线性系统的关键矩阵精确地算出来。此外,我们还讨论了HiPPO的离散化和相关性质等问题,这些内容奠定了后续的SSM工作的理论基础。
接下来,我们将介绍HiPPO的后续应用篇《Efficiently Modeling Long Sequences with Structured State Spaces》(简称S4),它利用HiPPO的推导结果作为序列建模的基本工具,并从新的视角探讨了高效的计算和训练方式,最后在不少长序列建模任务上验证了它的有效性,可谓SSM乃至RNN复兴的代表作之一。
基本框架
S4使用的序列建模框架,是如下的线性ODE系统:
\begin{equation}\begin{aligned}
x'(t) =&\, A x(t) + B u(t) \\
y(t) =&\, C^* x(t) + D u(t)
\end{aligned}\end{equation}
通向概率分布之路:盘点Softmax及其替代品
By 苏剑林 | 2024-06-14 | 13302位读者 | 引用不论是在基础的分类任务中,还是如今无处不在的注意力机制中,概率分布的构建都是一个关键步骤。具体来说,就是将一个$n$维的任意向量,转换为一个$n$元的离散型概率分布。众所周知,这个问题的标准答案是Softmax,它是指数归一化的形式,相对来说比较简单直观,同时也伴有很多优良性质,从而成为大部分场景下的“标配”。
尽管如此,Softmax在某些场景下也有一些不如人意之处,比如不够稀疏、无法绝对等于零等,因此很多替代品也应运而生。在这篇文章中,我们将简单总结一下Softmax的相关性质,并盘点和对比一下它的部分替代方案。
Softmax回顾
首先引入一些通用记号:$\boldsymbol{x} = (x_1,x_2,\cdots,x_n)\in\mathbb{R}^n$是需要转为概率分布的$n$维向量,它的分量可正可负,也没有限定的上下界。$\Delta^{n-1}$定义为全体$n$元离散概率分布的集合,即
\begin{equation}\Delta^{n-1} = \left\{\boldsymbol{p}=(p_1,p_2,\cdots,p_n)\left|\, p_1,p_2,\cdots,p_n\geq 0,\sum_{i=1}^n p_i = 1\right.\right\}\end{equation}
之所以标注$n-1$而不是$n$,是因为约束$\sum\limits_{i=1}^n p_i = 1$定义了$n$维空间中的一个$n-1$维子平面,再加上$p_i\geq 0$的约束,$(p_1,p_2,\cdots,p_n)$的集合就只是该平面的一个子集,即实际维度只有$n-1$。
重温SSM(二):HiPPO的一些遗留问题
By 苏剑林 | 2024-06-05 | 12518位读者 | 引用书接上文,在上一篇文章《重温SSM(一):线性系统和HiPPO矩阵》中,我们详细讨论了HiPPO逼近框架其HiPPO矩阵的推导,其原理是通过正交函数基来动态地逼近一个实时更新的函数,其投影系数的动力学正好是一个线性系统,而如果以正交多项式为基,那么线性系统的核心矩阵我们可以解析地求解出来,该矩阵就称为HiPPO矩阵。
当然,上一篇文章侧重于HiPPO矩阵的推导,并没有对它的性质做进一步分析,此外诸如“如何离散化以应用于实际数据”、“除了多项式基外其他基是否也可以解析求解”等问题也没有详细讨论到。接下来我们将补充探讨相关问题。
离散格式
假设读者已经阅读并理解上一篇文章的内容,那么这里我们就不再进行过多的铺垫。在上一篇文章中,我们推导出了两类线性ODE系统,分别是:
\begin{align}
&\text{HiPPO-LegT:}\quad x'(t) = Ax(t) + Bu(t) \label{eq:legt-ode}\\[5pt]
&\text{HiPPO-LegS:}\quad x'(t) = \frac{A}{t}x(t) + \frac{B}{t}u(t) \label{eq:legs-ode}\end{align}
其中$A,B$是与时间$t$无关的常数矩阵,HiPPO矩阵主要指矩阵$A$。在这一节中,我们讨论这两个ODE的离散化。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 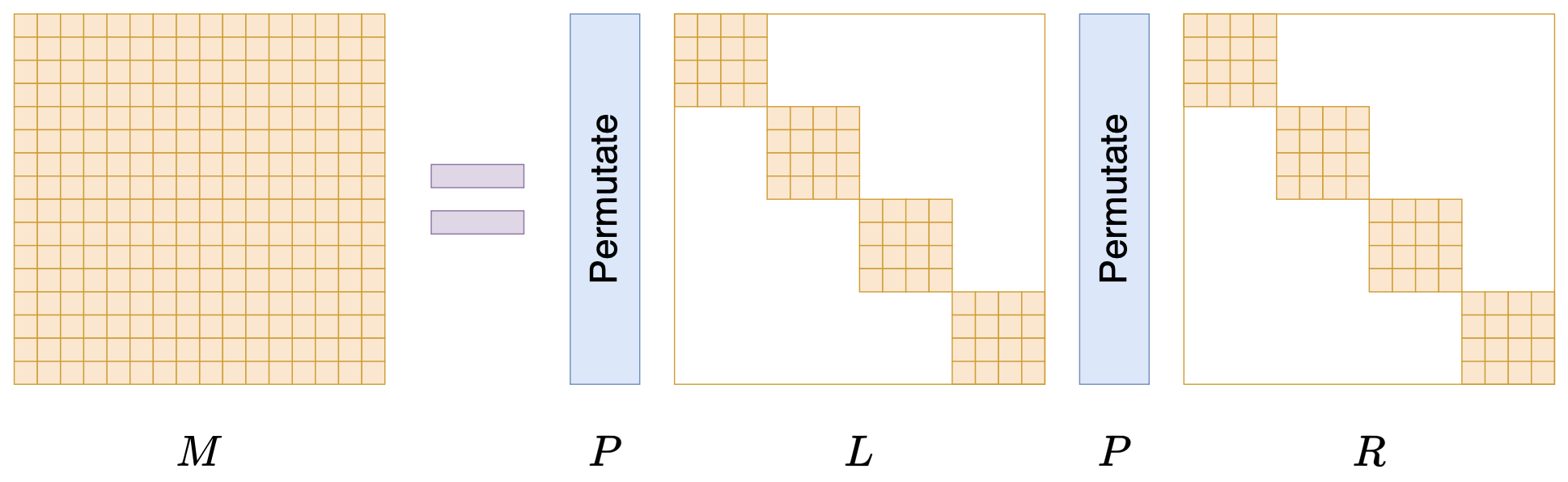


最近评论