为什么线性注意力要加Short Conv？

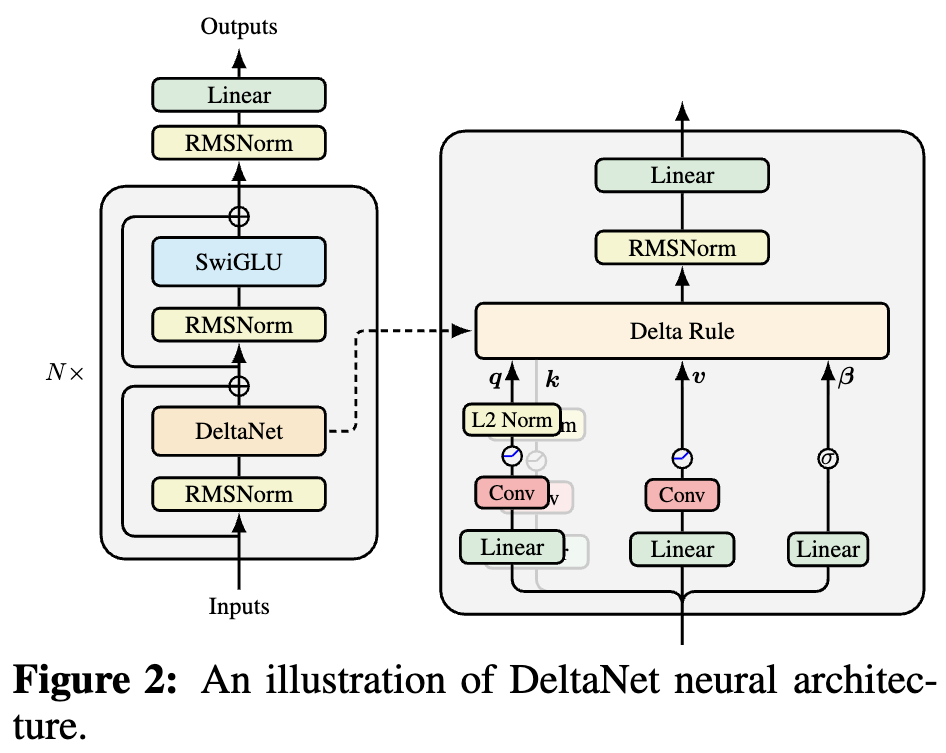
如果读者有关注模型架构方面的进展，那么就会发现，比较新的线性Attention（参考《线性注意力简史：从模仿、创新到反哺》）模型都给$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$加上了Short Conv，比如下图所示的DeltaNet：

为什么要加这个Short Conv呢？直观理解可能是增加模型深度、增强模型的Token-Mixing能力等，说白了就是补偿线性化导致的表达能力下降。这个说法当然是大差不差，但它属于“万能模版”式的回答，我们更想对它的生效机制有更准确的认知。

接下来，笔者将给出自己的一个理解（更准确说应该是猜测）。

测试训练 #

从《线性注意力简史：从模仿、创新到反哺》我们知道，目前的新式线性Attention背后的核心思想都是TTT（Test Time Training）或者说Online Learning。TTT基于优化器更新与RNN迭代的相似性，通过优化器来构建（不一定是线性的）RNN模型，诸如DeltaNet、GDN、Comba等线性Attention都可以看成它的特例。

具体来说，TTT将$\boldsymbol{K},\boldsymbol{V}$视为成对的语料$(\boldsymbol{k}_1, \boldsymbol{v}_1),(\boldsymbol{k}_2, \boldsymbol{v}_2),\cdots,(\boldsymbol{k}_t, \boldsymbol{v}_t)$，我们用它训练一个模型$\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$，然后输出$\boldsymbol{o}_t = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{q}_t)$，其中$\boldsymbol{S}_t$是模型参数，用SGD更新：
\begin{equation} \boldsymbol{S}_t = \boldsymbol{S}_{t-1} - \eta_t\nabla_{\boldsymbol{S}_{t-1}}\mathcal{L}(\boldsymbol{f}(\boldsymbol{S}_{t-1};\boldsymbol{k}_t), \boldsymbol{v}_t)\end{equation}
当然，如果我们愿意，也可以考虑其他优化器，比如《Test-Time Training Done Right》尝试了Muon优化器。除了可以改变优化器外，可以灵活改变的地方还有模型$\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$的架构以及损失函数$\mathcal{L}(\boldsymbol{f}(\boldsymbol{S}_{t-1};\boldsymbol{k}_t), \boldsymbol{v}_t)$。此外，我们还可以考虑以Chunk为单位的Mini-batch TTT。

不难想象，理论上TTT的灵活性非常高，可以构建任意复杂的RNN模型。当架构选择线性模型$\boldsymbol{v} = \boldsymbol{S}_t\boldsymbol{k}$且损失函数选择平方误差时，结果对应DeltaNet；如果我们加上一些正则项，那么可以衍生出GDN等变体。

灵魂拷问 #

将TTT放在前面，主要是想表明，当前主流的线性Attention的底层逻辑跟TTT一样，核心都是语料对$(\boldsymbol{k}_1, \boldsymbol{v}_1),(\boldsymbol{k}_2, \boldsymbol{v}_2),\cdots,(\boldsymbol{k}_t, \boldsymbol{v}_t)$的Online Learning。这就很自然地引申出一个疑问：为什么要这样做？这样做究竟学出个什么来？

要回答这个问题，首先得反思一下“我们究竟想要什么”。按照Softmax Attention的特点，我们想要的应该是根据$(\boldsymbol{k}_1, \boldsymbol{v}_1),(\boldsymbol{k}_2, \boldsymbol{v}_2),\cdots,(\boldsymbol{k}_t, \boldsymbol{v}_t)$和$\boldsymbol{q}_t$算出一个$\boldsymbol{o}_t$来，这个过程理想情况下应该依赖于全体$(\boldsymbol{k},\boldsymbol{v})$。同时，我们还希望能常数复杂度实现这个目标，所以一个直观想法是先将$(\boldsymbol{k},\boldsymbol{v})$压缩成（与$t$无关的）固定大小的State，然后再读取这个State。

怎么实现这个压缩呢？TTT的想法是：设计一个模型$\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$，然后用这些$(\boldsymbol{k},\boldsymbol{v})$对去“训练”这个模型，训练完成后，模型某种意义上就“背下”了这些$(\boldsymbol{k},\boldsymbol{v})$对，这就相当于就全体$(\boldsymbol{k},\boldsymbol{v})$压缩到了固定大小的模型权重$\boldsymbol{S}_t$中。至于$\boldsymbol{q}
_t$怎么利用$\boldsymbol{S}_t$，直接将它代入模型中得到$\boldsymbol{o}
_t = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{q}_t)$是一个比较自然的选择，但原则上我们也可以设计别的利用方式。

也就是说，TTT的核心任务是利用“训练模型”约等于“背诵训练集”这件事情，来实现$\boldsymbol{K},\boldsymbol{V}$的压缩。然而，“训练模型”约等于“背诵训练集”这件事情并不是那么平凡，它有一些前提条件。

键值同源 #

举个例子，如果我们取$\boldsymbol{K}=\boldsymbol{V}$，那么TTT这套框架理论上就失效了，因为这时候模型$\boldsymbol{v} = \boldsymbol{f}(\boldsymbol{S}_t;\boldsymbol{k})$的最优解就是恒等变换，它是一个平凡解，这相当于没记住任何东西。像DeltaNet这种在线更新的或许还能抢救一下，而像MesaNet这种基于准确解的就真的直接输出单位阵$\boldsymbol{I}$了。

可能有读者会反问：好端端地为啥要考虑$\boldsymbol{K}=\boldsymbol{V}$这种不科学的选择呢？的确，$\boldsymbol{K}=\boldsymbol{V}$是比较极端的选择，这里只是作为一个例子，说明“训练模型”约等于“背诵训练集”并不是随意成立的。其次，我们在《Transformer升级之路：20、MLA好在哪里?（上）》已经验证过，对于Softmax Attention来说，$\boldsymbol{K}=\boldsymbol{V}$也能取得不错的结果。

这说明，$\boldsymbol{K}=\boldsymbol{V}$并不是Attention机制的本质障碍，但在TTT框架里边它却能导致模型失效，这是因为$\boldsymbol{K},\boldsymbol{V}$完全重合，那么它们俩之间的回归就没有东西可学了。类似地，我们可以想象，$\boldsymbol{K},\boldsymbol{V}$的信息重合度越高，那么它们之间可学的东西就越少，换言之TTT对“训练集”的记忆程度就越低。

在一般的Attention机制中，$\boldsymbol{q}_t,\boldsymbol{k}_t,\boldsymbol{v}_t$都是由同一个输入$\boldsymbol{x}_t$经过不同的线性投影得到的，换句话说$\boldsymbol{k}_t,\boldsymbol{v}_t$具有相同的源头$\boldsymbol{x}_t$，这就始终有种“自己预测自己”的感觉，可学的东西有限。

卷积救场 #

怎么让TTT在键值同源甚至$\boldsymbol{K}=\boldsymbol{V}$时能学出更有价值的结果呢？其实答案很早就有了——可以追溯到Word2Vec甚至更早的年代——那就是不要“预测自己”，而是“预测周围”。

以Word2Vec为例，我们知道它的训练方式是“中心词预测上下文”；之前流行的BERT，预训练方式是MLM，它是某些词Mask掉来预测这些词，可以说是“上下文预测中心词”；现在主流的LLM，训练任务则是NTP（Next Token Predict），根据上文预测下一个词。很明显，它们的共同特点都是不预测自己，而是预测周围。

所以，想要改进TTT，那么就要改变$(\boldsymbol{k}_t,\boldsymbol{v}_t)$这样的“自己预测自己”的配对方式，考虑到当前LLM以NTP为主，在TTT中我们也可以考虑NTP，比如$(\boldsymbol{k}_{t-1},\boldsymbol{v}_t)$来构建语料对，即用$\boldsymbol{k}_{t-1}$来预测$\boldsymbol{v}_t$，这样即便$\boldsymbol{K}=\boldsymbol{V}$也能学出非平凡的结果。此时TTT内外都是NTP任务，具有漂亮的一致性。

不过，只用$\boldsymbol{k}_{t-1}$预测$\boldsymbol{v}_t$的话，似乎把$\boldsymbol{k}_t$浪费掉了，所以进一步的想法是把$\boldsymbol{k}_{t-1}$和$\boldsymbol{k}_t$以某种方式混合起来再预测$\boldsymbol{v}_t$。到这里，大家可能反应过来了，“把$\boldsymbol{k}_{t-1}$和$\boldsymbol{k}_t$以某种方式混合起来”这不就相当于kernel_size=2的Conv嘛！所以，给$\boldsymbol{K}$加Short Conv，是将TTT的训练目标从“预测自己”转化为NTP，让TTT至少有能力学出一个n-gram模型。

至于给$\boldsymbol{Q},\boldsymbol{V}$加Short Conv，则完全是顺带的，根据飞来阁（FLA群）的消息，给$\boldsymbol{Q},\boldsymbol{V}$加虽然也有一点作用，但远不如给$\boldsymbol{K}$加Short Conv带来的提升，这也算是佐证了我们的猜测。

文章小结 #

这篇文章对“为什么线性注意力要加Short Conv”这个问题给出了一个闭门造车的理解。

转载到请包括本文地址：https://www.spaces.ac.cn/archives/11320

更详细的转载事宜请参考：《科学空间FAQ》