数学竞赛广东预赛|组成三角形的概率
By 苏剑林 | 2011-09-12 | 74088位读者 |九月三日BoJone和九个同学到云浮参加了今年广东省的数学竞赛预赛,那一起出发、玩笑、作战、吃饭的情景依然历历在目,让我久久不能忘怀。是呀,能够并肩作战的感觉真好!九日数学成绩出来了,遗憾的是今年政策改变了,我被告知整个市只有三个名额能够参加复赛,于是新兴只有我一个人进入了复赛(另外两个据说是罗定的,我们三个并列第一)。有点无语,我想,大概是要把那些为了功利而参赛的人都给刷下去吧...
今年广东的预赛题前所未有的简单,不论是和全国其他地方相比还是和上一年的题目相比,都简单了不少,但我还是做得不大理想,据我估计,120分的卷子我顶多能够拿个68分,所以BoJone的基本技能实在不容乐观。从云浮考试回来后,和同行的同学讨论试题,得出了一些很有趣的结果,那过程可谓其乐无穷呀!下面是倒数第二题预赛题的几个绝妙解法,供大家欣赏。解法由我和伍泽麒(人称“兔子、神兔”,人如其名,天资聪颖,性格可爱)完成。
题目:
在一条线段中随意选取两个点,把这条线段截成三段,求这三段线段能够组成一个三角形的概率。
题目很容易看明白,答案也很简单,是1/4。这种题目常规的思路是线性规划,但线性规划是一种代数思想,属于解析几何的范畴。而1/4这个答案是如此简洁,甚至让我们感到线性规划做法过于“丑陋”了,我们应该寻找到更简明、更直接的思路,并希望能向纯几何思路靠拢。正是因为这一思想,下面的三种解法诞生了。
一、圆形、对称思想
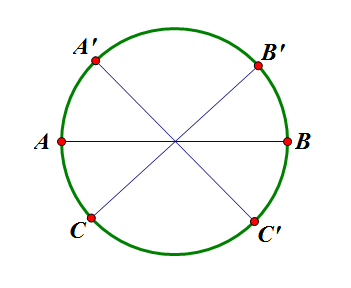
将所要截的线段首尾相连摆成一个圆,设A为连接点,并设另外两个截点为C和D,只要A、C、D不在同一个半圆内,就可以将圆拉直为ΔACD。如图,AB为直径,那么C、D必须被AB分隔开来,这样的概率是1/2(C、D同在AB下方的概率是1/4,上方亦然)。
在圆上任意选取一点C,则D的取值区域为劣弧BB',同时可以找到对应的另外一点C',使得D的不可取值区域为劣弧AA',其中AC=BC',BB'=AA',则在1/2概率中,能够组成三角形和不能够组成三角形的情况是一一对应的,那就说明它们的概率相等,即各占一半,于是能够组成三角形的概率为$P(\Delta)=1/2 \cdot 1/2 = 1/4$。
二、椭圆、圆思想
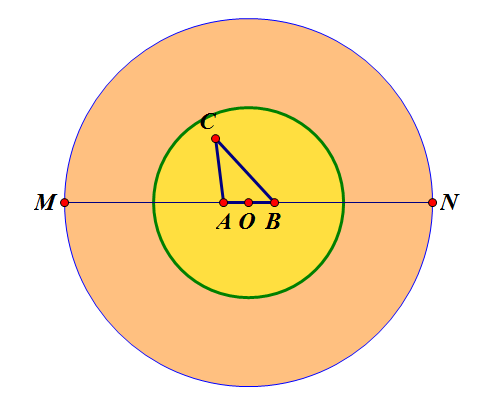
周长固定的三角形,固定其中两点,第三点随意运动,描绘出来的轨迹是一个椭圆。根据这个原理,我们分别以线段长度以及长度的一半作同心圆。设线段AD被截成了AB、BC、CD三段,令AB段与直径MN重合,其中点与O点重合。那么只有当C点在小圆内时,才可以找到对应的AB段组成一个三角形(找到相应的椭圆即可),当C点在小圆外大圆内时,无法找到AB段组成一个定周长的三角形。于是可以组成三角形的概率等于S小圆/S大圆=1/4.
三、三角坐标系思想
三角坐标系这个思想很具有代表性,不过它的思路来源倒不是数学,而是地理。的确,我第一次看到它的时候是在地理试卷,那种描述一个国家地区的幼年、中年、老年人口比例的图,这三个比例有一个特点,那就是它们的和等于1。而本文所探讨的三角形也有类似的性质:三边之和为定值。这就给了我一点启示。
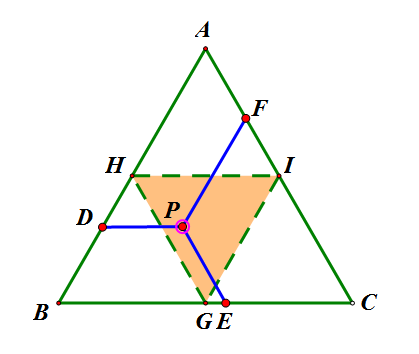
如图,以线段长为边长作等边三角形ABC,并作如图所示的D、E、F点,可见PD+PE+PF=AB,且PD=AF,PF=CE,PE=BD。则要组成三角形,只需要满足任意两边之和大于第三边,也就是每一边都小于$1/2 AB$即可。从图中可以看出,只要AF、CE、BD有一边大于$AB/2$,那么P点必然落在了三角形GHI外,因此要组成三角形,P点必须在三角形GHI内,于是组成三角形的概率:
$$P(\Delta)=\frac{S_{\Delta GHI}}{S_{\Delta ABC}}=1/4$$
解法介绍完毕。
以上就是我们班同学在探讨题目过程中得出的三种解法,每一种解法都尽量靠近纯几何,并使思路尽可能地明显,在欣赏数学简洁美的同时,企图让大家觉得思路的必然性。当然,这只是冰山一角,希望经过抛砖而引出玉来。如果各位读者有更好的解法,欢迎交流。在此,科学空间祝大家中秋节快乐!
转载到请包括本文地址:https://www.spaces.ac.cn/archives/1477
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 12, 2011). 《数学竞赛广东预赛|组成三角形的概率 》[Blog post]. Retrieved from https://www.spaces.ac.cn/archives/1477
@online{kexuefm-1477,
title={数学竞赛广东预赛|组成三角形的概率},
author={苏剑林},
year={2011},
month={Sep},
url={\url{https://www.spaces.ac.cn/archives/1477}},
}










September 16th, 2011
哇!!!搞竞赛的伤不起啊。。。
以前我也参加过数学竞赛,但是水平实在是太菜,题目实在是只有某些中国专家才能做出来!
我参加信息学奥赛的时候,当时云浮市只有我一个人进了复赛。
我的水平也很低,很多题目都不会...当年原来你还获得了信息赛的加分呀,这么好!那时候就已经初露锋芒了^_^
September 23rd, 2011
竞赛...伤痛了么...
物理竞赛因为学校没报名(还和我说会报的..)(魂淡,都有责任..)没去参加啊~~
化学裸考,16分...太悲惨了...
数学没胆量去参加,那个一定更加悲催的...
替你感到悲剧...
我参加数学竞赛了,现在准备复赛,不过看似希望渺茫...
加油哦~~
October 1st, 2011
第三种解法构思巧妙,方法一目了然,让人拍案叫绝。因为自己水平不够,第一、二种解法到现在还是看不明白。不过正因为自己的水平不够,所以对常规的代数解法就尤其感兴趣了。我自己试了一下。设线段长度为1,当第一点取值范围在(0 , 0.5)之间,其坐标为x时,第二点只能在(0.5, 0.5+x)之间取,其概率为(0.5+x)-0.5=x, xdx在(0 , 0.5)之间积分,为0.125。当第一点取值范围在(0.5 , 1)之间,其坐标为x时,第二点只能在(x-0.5, 0.5)之间取,其概率为0.5-(x-0.5)=1-x, (1-x)dx在(0.5 , 1)之间积分,亦为0.125,两个概率相加,即为1/4。但,这是我后来的做法。开头我是这样做的,由于这两点中右边的那点只能在(0.5,1)之间取值,设其坐标为x时,则左边那点只能在(x-0.5, 0.5)之间取,其概率为0.5-(x-0.5)=1-x, (1-x)dx在(0.5 , 1)之间积分,为0.125,这样概率只是1/8——错在哪里呢?开头我百思不得其解,后来终于想明白了,这个1/8还必须除以xdx在(0,1)之间的积分(这个积分的数值是1/2,所以除完就变成1/4了)。班门弄斧的问一下大家,为什么要这样做?
接着继续班门弄斧一下。三个变量的和为一定值时可以用三角坐标系,那四个变量的和为一定值时需用什么坐标系?由此引申出另一个问题——在一条线段中间随机取三点将其分成四段,这四条小线段能够组成四边形的概率是多少(如果我没想错,应该是1/8)。
最后向Bojone同好请教一个问题。1dx在[0,1]之间的积分,和1dx在(0,0.5)(0.5,1)这样一个分成两个开区间的定义域中的积分结果是不是相等的?
按照类比思想,四个变量的和恒定,可以这样构思:正四面体中的一点到四个面的距离之和恒定。
组成四边形,只需要三条短边之和大于最长边就行了吧?可以类似一下第三种解法,构造一个正四面体...大概是这样吧,没有多想。不过用立体的思路来解决平面体,有点杀鸡用牛刀的感觉。
至于后边的问题答案是肯定的。
因为你的最初做法中,暗含了右边那点(记为y)和左边那点(x)的一个关系:y > x,所以1/8的那块“可行区域”中,它的“可选区域”不是0到1的那个小正方形,而是由不等式数1 > y > x > 0决定的一个三角形区域(面积为1/2)。
October 1st, 2011
另外,其实第二种做法的解释比较勉强,但是第一种解法其实也是很“显然”的,最后用到的对应思想也是一种十分重要的思想。
October 25th, 2011
第三种方法非常妙!
June 26th, 2015
第一个解法挺帅.第二个看不懂椭圆还没学。。第三个太牛了,真希望考试考这道题然后我用大牛的方法来解