浅谈引力助推

这已经是去年写的稿件了，刊登在今年二月份的《天文爱好者》上，本文的标题还登载了该期天爱的封面上，当时甚是高兴呢！在此与大家分享、共勉。

相信许多天文爱好者都知道第一、第二、第三宇宙速度的概念，也会有不少的天爱自己动手计算过它们。我们道，只要发射速度达到7.9km/s，宇宙飞船就可以绕地球运行了；超过11.2km/s，就可以抛开地球，成为太阳系的一颗“人造行星”；再大一点，超过16.7km/s，那么就连太阳也甩掉了，直奔深空。

16.7km/s，咋看上去并不大，因为地球绕太阳运行的速度已经是30km/s了，这个速度在宇宙中实在是太普通了。但是对于我们目前的技术来说，它大得有点可怕。维基百科上的资料显示，史上最强劲的火箭土星五号在运送阿波罗11号到月球时，飞船最终也只能加速到接近逃逸速度，即11.2km/s，而事实上第三宇宙速度已经是是目前人造飞行器的速度极限了。可是没有速度，我们就不能发射探测器去探索深空，那些科幻小说中的“星际移民”，就永远只能停留在小说上了。

引力助推的历史渊源

真的一点办法都没有吗？不一定。我们自己在地球上没有办法实现，但可以让其他星球助我们一臂之力！这就是引力助推(Gravity Assist)，物理上也叫弹弓效应。最初提出引力助推法的科学家是苏联的尤里?康德拉图克(Кондратюк, Юрий Васильевич)。他在所署时间为“1918-1919”[2]的论文“Тем кто будет читать, чтобы строить”（《致有志于建造星际火箭而阅读此文者》）中提出在两颗行星间飞行的飞船可以使用两行星的引力实现轨道初段的加速和轨道末段的减速。弗里德里希?詹德(Friedrich Zander)在其1925年的论文“Проблема полета при помощи реактивных аппаратов: межпланетные полеты”（《星际飞行中喷气推进的问题》）中也提出了类似的构想。1959年，引力推进法得到了首次应用，当时苏联的探测器月球3号使用该法运行至月球背面并拍摄了该区域的照片。当时这一操作流程由克尔德什应用数学研究所所设计。但是两者都未能意识到行星沿飞行器轨道施加的引力助推能够推进飞行器从而减少飞行器星际间飞行的燃料消耗。而第一个意识到这一重要作用的是UCLA研究生迈克尔?米诺维奇(Michael Minovitch)。

1961年，25岁的Michael Minovitch对大学的新IBM 7090计算机兴奋不已，它是当时世界上最快的计算机，他于是决定在计算机上研究天体力学中的最大难题“三体问题”。利用计算机，Minovitch的迭代模型取得了一些突破。他发现，一艘飞船飞经绕日行星，可以在不使用任何火箭燃料的情况下窃取行星的一点轨道速度加速离开太阳。1965年夏天，Minovitch考虑是否可以将他的发现运用于实践。结果是让人惊喜的，他得知1970年代后期，木星、土星、天王星和海王星都将位于太阳的同一侧，如果一艘飞船能在1977年发射升空，它将可以在12年内经过四大行星，类似的机会要过176年才会再次发生。在Minovitch的游说和高层的干预下，美国开始了航海家号计划。至今，NASA的两艘航海家号飞船已经发射了35年，抵达了太阳系的边缘，其中航海家一号距离地球184亿千米，它将成为第一个离开太阳系的人造飞行器。

物理原理

这样看来，引力助推真的非常有趣，它能够巧妙地从行星身上“揩油”，以增加自身的速度。这里面涉及到了物理上的动量守恒定律，我们可以用一个简单的例子来展示这种效果。设想一列火车正以100km/h的速度向左开去，有一个篮球也正以100km/h的速度向右飞去（这个速度夸张了点，但是我只是为了展示这种效应而已），那么，两者相撞之后，会发生什么事情呢？火车自然是毫发无损，继续以100km/h的速度向左开着；但可怜的篮球会以更高的速度被反弹（假如它质量非常非常好）。那么这个速度是多少呢？可以这样分析：如果把火车看成静止的，那么篮球向火车飞来的速度就是200km/h，它撞上火车，应该会以原速度反弹，即200km/h；但这个200km/h是在一列100km/h运行的火车上测量的，所以它的实际速度应该是300km/h！

真不可思议，这样绕了一个圈，速度居然增加了200km/h！也就是说，它可以“揩”到运动主体的速度两倍的“油”！有些读者可能会疑惑，这多出来的200km/h好像是无中生有的，它不满足能量守恒定律呀。其实，上面那个变换参考系的做法，是一个近似做法，因为火车的质量比篮球的质量大得多，所以可以这样做。实际上火车的速度或减少一点点，而篮球的速度也达不到300km/h，但是已经非常接近了。

这与天文上的引力助推有什么关系呢？我们总不能让一个飞行器撞上一颗行星然后让它反弹回来吧？科学家有一个非常巧妙的方法，由于行星的引力作用，它会把飞行器拉向自身，然后再对称地甩出去，这一过程和上例中的反弹时等价的。事实证明如果飞行器沿双曲线轨道运行，则其无需启动引擎即可从相反方向离开行星，同时只要其脱离了该行星引力的控制，那么它就可以获得2倍的速度增量。

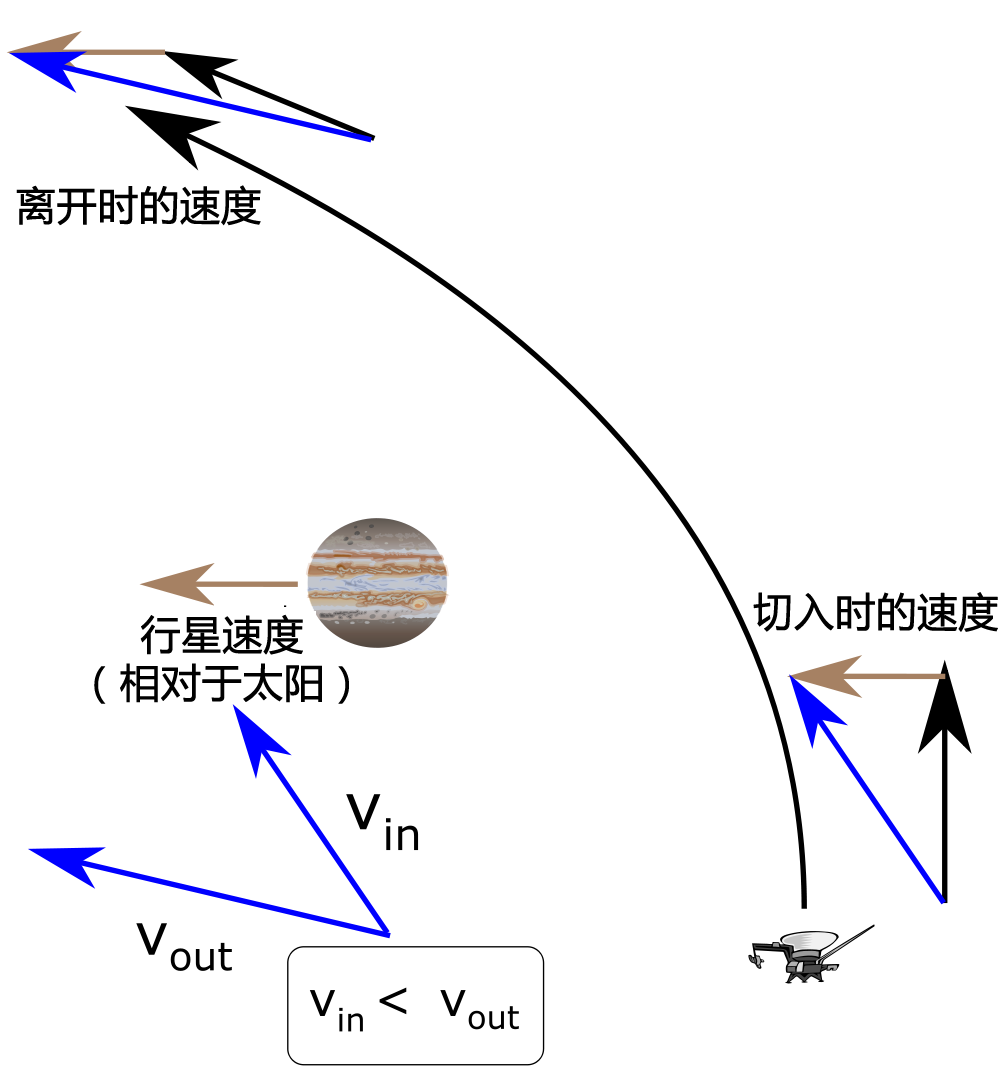
当然，在现实宇宙空间中，飞行器与行星的相遇实际上是二维的。在上述理论所提供的案例中，由于要求提高飞行器的速度，所以需要实现的是矢量增益，如下图所示。

如果飞行器需要获得更大的动能，最经济的做法是当其位于行星近拱点时点燃火箭。火箭助推为飞行器提供的加速度总是相同的，但是它引起的动能变化则与飞行器的实时速度成正比。这叫奥伯特效应。举个简单的例子，用1N的力作用于1kg的物体，每秒钟增加的速度为1m/s，当初速度是5m/s时，增加的动能就是(62-52)/2=5.5J，但是初速度是10m/s时，增加的动能是(11²-10²)/2=10.5J，近似两倍。所以为了从火箭助推中获得最大动能，火箭必须在飞行器速度最大时——即处于近拱点时点火。

实际应用

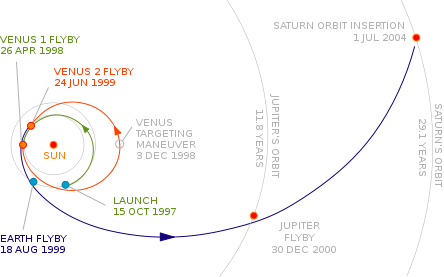
可以说，目前所有的外行星探索活动，全都离不开引力助推技术。除了航海家号，最典型的一个例子就是探索土星的卡西尼了。根据引力助推原理，科学家们为“卡西尼”号设计了一条通往土星的智慧曲线，这条智慧曲线的奇特之处在于：首先是它没有直接向土星飞去，而是先向内跑到了金星上空；其次是它围绕地球绕了好几个圈子，才把目的地对准土星，整个行程达到了35.2亿千米，是地球与土星的实际距离的2.5倍以上。它的飞行轨迹是一条旋转的曲线，是若干条双曲线截线的组合，看起来就像田螺背上的螺旋。

不过，引力助推到不一定总是用于加速飞行器的，有时也会用于减速。因为地球本身已经有30km/s的速度了，要飞往地内行星，这个速度已经太大了，需要反方向减速，引力助推也能实现这个效果。1974年的水手10号以及后来的信使号即通过引力助推实现了减速，两者都是飞往水星的探测器。此外，条件适宜的情况下，大气制动也可用来实现飞行器的减速。如果两者可以有机结合起来，往往减速效果更好。

除此之外，水手10号、旅行者1号、伽利略号、尤利西斯号探测器、信使号等探测器的飞行过程中都是用了引力助推技术。在未来的星际探索中，也是我们会使用太阳作为助推星体，但是探索太阳系是不可行的，因为太阳相对于太阳系几乎是静止的。

更有趣的是，引力助推并不是人类的专利，一些小行星偶然也可能掠过大行星而实现自身加速。比如近地小行星3753通过引力助推与地球交换能量，从而周期性地改变轨道。

当然，引力助推法也有一定的缺陷，有时为了等待行星达到适合的位置，就有可能干耗掉几年；为了实现更好的加速效果，通常要让飞行器更加接近行星，以获得更大的引力作用。但是越靠近行星，行星的大气又会导致减速，这是一个永远的矛盾。但是不论如何，目前来说它还是一种非常经济可行的方案。

延伸阅读：非碰撞奇点——有限时间内飞到无穷远处

说完引力助推，再来说说N体问题中与此相关的“非碰撞奇点”问题。我们研究引力助推，就是希望缩短飞行时间，如果现在告诉你，利用引力助推，可以在有限的时间内飞到无穷远处，你会不会立马兴奋起来？

这就是N体问题中研究的“非碰撞奇点”问题。当然，这是在非相对论的情况下讨论的，而且并不是在任意情况下都可以实现的。这个问题首先由一位与庞加莱同时代的法国数学家庞勒维（Paul Painleve）正式提出，他猜测这样的解释存在的，这被称为“庞勒维猜想”。让人意外的是，真的存在这样的系统，经过巧妙地设置后，某一个天体在有限时间内就飞到无穷远了。首先肯定回答这个问题的，竟是一位二十来岁的中国数学家——夏志宏，而此时距离问题提出的时间，已经接近百年了。

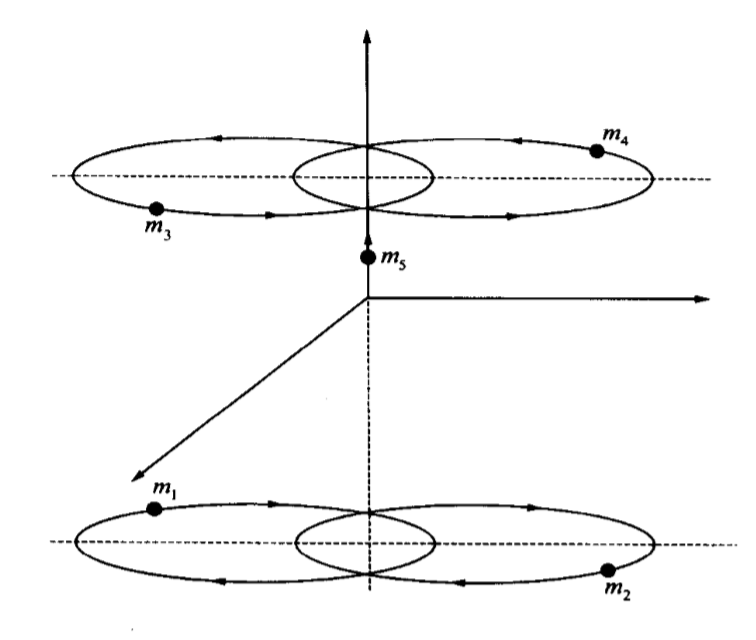
夏志宏巧妙地构造了一个系统，如图所示，有四个质量相同的天体m₁,m₂,m₃,m₄，其中m₁,m₂在下方做顺时针的高偏心率椭圆运动，而m₃,m₄在上方做逆时针的高偏心率椭圆运动，它们具有大小相同反向相反的角速度。小质量天体m₅位于两个二体系统的中轴线上，在两个二体系统之间来回振荡。m₅每次穿过上平面从而进入两平面之间时，二体系统的两个天体刚好达到最近，于是在强烈的引力作用下，m₅由引力助推产生巨大加速度，由动量守恒定律，m₁,m₂被迫上升；然后再穿过另外一个二体平面，导致m₃,m₄被迫下降。如此往返，每一次m5都从二体系统身上窃取了巨大的加速度，导致它们的能量不断减少，也就是说，m₁与m₂、m₃与m₄的距离会趋于无穷小（两天体的距离越小，引力势能也越小），但是换来的后果是——两个二体系统之间的距离在有限时间内得到无穷远了。

当夏志宏提出这个解时，数学界和天文界第一反应不是兴奋，而是惊疑：这么重要的问题居然被一个二十来岁的学生解决了？但是经过重重审核，答案出来了：结论是正确的。这个伟大的成为被称誉为“夏氏定理”！这个结果的构造充分体现了夏志宏惊人的创造力，他几乎综合了一百年来所有天体力学的成就，而且提出了不少新的思想，才得到这个答案。换句话说，他“站在了无数巨人的肩膀上”，做出了自己杰出的成果。这对我们学习也具有重要的指导意义：不积跬步，无以至千里；不积小流，无以成江海。

不过，这毕竟仅仅是一个数学上的玩意，实际意义似乎没有。但不论如何，在这个问题上，彰显了中国年轻数学家的巨大创造力。同时，它作为一件精美的艺术品，让我们欣赏，让我们惊叹N体问题的神奇，也惊叹引力助推的巨大力量。在拥有引力的世界里，真可谓“无奇不有”！

参考资料：
科普书《天遇：混沌与稳定性的起源》
维基百科：http://en.wikipedia.org/wiki/Gravity_assist

引力助推专题：http://www.gravityassist.com/

引力助推模拟：
http://messenger-education.org/Interactives/ANIMATIONS/grav_assist/gravity_assist.html

转载到请包括本文地址：https://www.spaces.ac.cn/archives/1953

更详细的转载事宜请参考：《科学空间FAQ》