细水长flow之f-VAEs:Glow与VAEs的联姻
By 苏剑林 | 2018-09-21 | 188700位读者 |这篇文章是我们前几天挂到arxiv上的论文的中文版。在这篇论文中,我们给出了结合流模型(如前面介绍的Glow)和变分自编码器的一种思路,称之为f-VAEs。理论可以证明f-VAEs是囊括流模型和变分自编码器的更一般的框架,而实验表明相比于原始的Glow模型,f-VAEs收敛更快,并且能在更小的网络规模下达到同样的生成效果。
原文地址:《f-VAEs: Improve VAEs with Conditional Flows》
近来,生成模型得到了广泛关注,其中变分自编码器(VAEs)和流模型是不同于生成对抗网络(GANs)的两种生成模型,它们亦得到了广泛研究。然而它们各有自身的优势和缺点,本文试图将它们结合起来。
基础 #
设给定数据集的证据分布为$\tilde{p}(x)$,生成模型的基本思路是希望用如下的分布形式来拟合给定数据集分布
$$\begin{equation}q(x)=\int q(z)q(x|z) dz\end{equation}$$
其中$q(z)$一般取标准高斯分布,而$q(x|z)$一般取高斯分布(VAEs中)或者狄拉克分布(GANs和流模型中)。理想情况下,优化方式是最大化似然函数$\mathbb{E}[\log q(x)]$,或者等价地,最小化$KL(\tilde{p}(x)\Vert q(x))$。
由于积分可能难以显式计算,所以需要一些特殊的求解技巧,这导致了不同的生成模型。其中,VAE引入后验分布$p(z|x)$,将优化目标改为更容易计算的上界$KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))$。众所周知,VAE有着收敛快、训练稳定等优点,但一般情况下生成图像存在模糊等问题,其原因我们在后面会稍加探讨。
而在流模型中,$q(x|z)=\delta(x - G(z))$,并精心设计$G(z)$(通过流的组合)直接把这个积分算出来。流模型的主要组件是“耦合层”:首先将$x$分区为两部分$x_1,x_2$,然后进行如下运算
$$\begin{equation}\begin{aligned}&y_1 = x_1\\
&y_2 = s(x_1)\otimes x_2 + t(x_1)
\end{aligned}\label{eq:coupling}\end{equation}$$
这个变换是可逆的,逆变换为
$$\begin{equation}\begin{aligned}&x_1 = y_1\\
&x_2 = (y_2 - t(y_1)) / s(x_1)
\end{aligned}\end{equation}$$
它的雅可比行列式是$\prod_i s_i(x_i)$。这种变换我们通常称之为“仿射耦合”(如果$s(x_1)\equiv 1$,那么通常称为“加性耦合”),用$f$表示。通过很多耦合层的组合,我们可以得到复杂的非线性变换,即$G = f_1 \circ f_2 \circ \dots \circ f_n$,这就是所谓的“(无条件)流”。
由于直接算出来积分,因此流模型可以直接完成最大似然优化。最近发布的Glow模型显示出强大的生成效果,引起了许多人的讨论和关注。但是流模型通常相当庞大,训练时间长(其中256x256的图像生成模型用40个GPU训练了一周,参考这里和这里),显然还不够友好。
分析 #
VAEs生成图像模糊的解释有很多,有人认为是mse误差的问题,也有人认为是KL散度的固有性质。但留意到一点是:即使去掉隐变量的KL散度那一项,变成普通的自编码器,重构出来的图像通常也是模糊的。这表明,VAEs图像模糊可能是低维重构原始图像的固有问题。
如果将隐变量维度取输入维度一样大小呢?似乎还不够,因为标准的VAE将后验分布也假设为高斯分布,这限制了模型的表达能力,因为高斯分布簇只是众多可能的后验分布中极小的一部分,如果后验分布的性质与高斯分布差很远,那么拟合效果就会很糟糕。
那Glow之类的流模型的问题是什么呢?流模型通过设计一个可逆的(强非线性的)变换将输入分布转化为高斯分布。在这个过程中,不仅仅要保证变换的可逆性,还需要保证其雅可比行列式容易计算,这导致了“加性耦合层”或“仿射耦合层”的设计。然而这些耦合层只能带来非常弱的非线性能力,所以需要足够多的耦合层才能累积为强非线性变换,因此Glow模型通常比较庞大,训练时间较长。
f-VAEs #
我们的解决思路是将流模型引入到VAEs中,用流模型来拟合更一般的后验分布$p(z|x)$,而不是简单地设为高斯分布,我们称之为f-VAEs(Flow-based Variational Autoencoders,基于流的变分自编码器)。相比于标准的VAEs,f-VAEs跳出了关于后验分布为高斯分布的局限,最终导致VAEs也能生成清晰的图像;相比于原始的流模型(如Glow),f-VAEs的编码器给模型带来了更强的非线性能力,从而可以减少对耦合层的依赖,从而实现更小的模型规模来达到同样的生成效果。
推导过程 #
我们从VAEs的原始目标出发,VAEs的loss可以写为
$$\begin{equation}\begin{aligned}&KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))\\
=&\iint \tilde{p}(x)p(z|x)\log \frac{\tilde{p}(x)p(z|x)}{q(x|z)q(z)} dzdx\end{aligned}\label{eq:vae-loss}\end{equation}$$
其中$p(z|x),q(x|z)$都是带参数的分布,跟标准VAEs不同的是,$p(z|x)$不再假设为高斯分布,而是通过流模型构建
$$\begin{equation}p(z|x) = \int \delta(z - F_x(u))q(u)du\label{eq:cond-flow}\end{equation}$$
这里$q(u)$是标准高斯分布,$F_x(u)$是关于$x,u$的二元函数,但关于$u$是可逆的,可以理解为$F_x(u)$是关于$u$的流模型,但它的参数可能跟$x$有关,这里我们称为“条件流”。代入$\eqref{eq:vae-loss}$计算得到
$$\begin{equation}\iint \tilde{p}(x)q(u)\log \frac{\tilde{p}(x) q(u)}{q(x| F_x(u))q(F_x(u))\left|\det \left[\frac{\partial F_x (u)}{\partial u}\right]\right|} dudx\label{eq:f-vae-loss}\end{equation}$$
这便是一般的f-VAEs的loss,具体推导过程请参考下面的注释。
联立$\eqref{eq:vae-loss}$和$\eqref{eq:cond-flow}$,我们有
$$\begin{equation}\begin{aligned}&\iiint \tilde{p}(x)\delta(z - F_x(u))q(u)\log \frac{\tilde{p}(x)\int\delta(z - F_x(u'))q(u')du'}{q(x|z)q(z)} dzdudx\\
=&\iint \tilde{p}(x)q(u)\log \frac{\tilde{p}(x)\int\delta(F_x(u) - F_x(u'))q(u')du'}{q(x| F_x(u))q(F_x(u))} dudx
\end{aligned}\label{eq:vae-loss-cond-flow}\end{equation}$$
设$v = F_x(u'), u'=H_x(v)$,对于雅可比行列式,我们有关系
$$\begin{equation}\det \left[\frac{\partial u'}{\partial v}\right]=1\Big/\det \left[\frac{\partial v}{\partial u'}\right]=1\Big/\det \left[\frac{\partial F_x (u')}{\partial u'}\right]\end{equation}$$
从而$\eqref{eq:vae-loss-cond-flow}$变成
$$\begin{equation}\begin{aligned}&\iint \tilde{p}(x)q(u)\log \frac{\tilde{p}(x)\int\delta(F_x(u) - v)q(H_x(v))\left|\det \left[\frac{\partial u'}{\partial v}\right]\right|dv}{q(x| F_x(u))q(F_x(u))} dudx\\
=&\iint \tilde{p}(x)q(u)\log \frac{\tilde{p}(x)\int\delta(F_x(u) - v)q(H_x(v))\Big/\left|\det \left[\frac{\partial F_x (u')}{\partial u'}\right]\right|dv}{q(x| F_x(u))q(F_x(u))} dudx\\
=&\iint \tilde{p}(x)q(u)\log \frac{\tilde{p}(x) q(H_x(F_x(u)))\Big/\left|\det \left[\frac{\partial F_x (u')}{\partial u'}\right]\right|_{v=F_x(u)}}{q(x| F_x(u))q(F_x(u))} dudx\\
=&\iint \tilde{p}(x)q(u)\log \frac{\tilde{p}(x) q(u)}{q(x| F_x(u))q(F_x(u))\left|\det \left[\frac{\partial F_x (u)}{\partial u}\right]\right|} dudx
\end{aligned}\end{equation}$$
两个特例 #
式$\eqref{eq:f-vae-loss}$描述了一般化的框架,而不同的$F_x(u)$对应于不同的生成模型。如果我们设
$$\begin{equation}\label{eq:vae-fxu} F_x(u)=\sigma(x)\otimes u + \mu(x)\end{equation}$$
那么就有
$$\begin{equation}-\int q(u)\log \left|\det \left[\frac{\partial F_x (u)}{\partial u}\right]\right| du=-\sum_i\log \sigma_i(x)\end{equation}$$
以及
$$\begin{equation}\int q(u)\log \frac{q(u)}{q(F_x(u))}du=\frac{1}{2}\sum_{i=1}^d(\mu_i^2(x)+\sigma_i^2(x)-1)\end{equation}$$
这两项组合起来,正好是后验分布和先验分布的KL散度;代入到$\eqref{eq:f-vae-loss}$中正好是标准VAE的loss。意外的是,这个结果自动包含了重参数的过程。
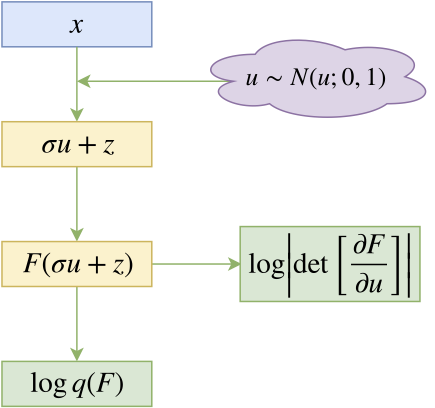
另一个可以考察的简单例子是
$$\begin{equation}\label{eq:flow-fxu} F_x(u)=F(\sigma u + x),\quad q(x|z)=\mathcal{N}(x;F^{-1}(z),\sigma^2)\end{equation}$$
其中$\sigma$是一个小的常数,而$F$是任意的流模型,但参数与$x$无关(无条件流)。这样一来
$$\begin{equation}\begin{aligned}&-\log q(x|F_x(u))\\
=& -\log \mathcal{N}(x; F^{-1}(F(\sigma u + x)),\sigma^2)\\
=& -\log \mathcal{N}(x; \sigma u + x,\sigma^2)\\
=& \frac{d}{2}\log 2\pi \sigma^2 + \frac{1}{2}\Vert u\Vert^2
\end{aligned}\end{equation}$$
所以它并没有包含训练参数。这样一来,整个loss包含训练参数的部分只有:
$$\begin{equation}-\iint \tilde{p}(x)q(u)\log q(F(\sigma u + x))\left|\det \left[\frac{\partial F(\sigma u + x)}{\partial u}\right]\right| dudx\end{equation}$$
这等价于普通的流模型,其输入加上了方差为$\sigma^2$的高斯噪声。有趣的是,标准的Glow模型确实都会在训练的时候给输入图像加入一定量的噪声。
我们的模型 #
上面两个特例表明,式$\eqref{eq:f-vae-loss}$原则上包含了VAEs和流模型。$F_x(u)$实际上描述了$u,x$的不同的混合方式,原则上我们可以选择任意复杂的$F_x(u)$,来提升后验分布的表达能力,比如
$$\begin{equation}\begin{aligned}&f_1 = F_1\Big(\sigma_1(x)\otimes u + \mu_1(x)\Big)\\
&f_2 = F_2\Big(\sigma_2(x)\otimes f_1 + \mu_2(x)\Big)\\
&F_x(u) = \sigma_3(x)\otimes f_2 + \mu_3(x)\end{aligned}\end{equation}$$
这里的$F_1, F_2$是无条件流。
同时,到目前为止,我们并没有明确约束隐变量$z$的维度大小(也就是$u$的维度大小),事实上它是一个可以随意选择的超参数,由此我们可以训练更好的降维变分自编码模型。但就图像生成这个任务而言,考虑到低维重构会导致模糊的固有问题,因此我们这里选择$z$的大小跟$x$的大小一致。
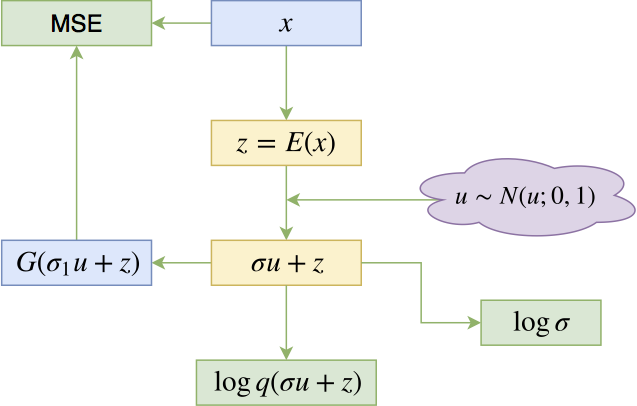
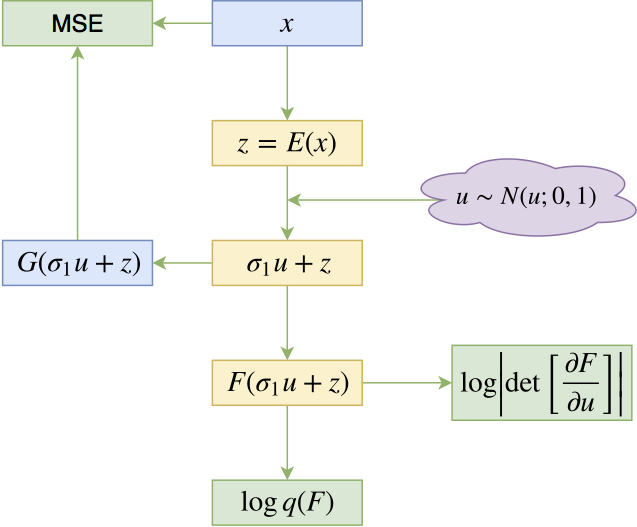
出于实用主义和简洁主义,我们把式$\eqref{eq:flow-fxu}$和$\eqref{eq:vae-fxu}$结合起来,选择:
$$\begin{equation}\label{eq:f-vae-fxu} F_x(u)=F(\sigma_1 u + E(x)),\quad q(x|z)=\mathcal{N}(x;G(F^{-1}(z)),\sigma_2^2)\end{equation}$$
其中$\sigma_1,\sigma_2$都是待训练参数(标量即可),$E(\cdot),G(\cdot)$是待训练的编码器和解码器(生成器),而$F(\cdot)$是参数与$x$无关的流模型。代入$\eqref{eq:f-vae-loss}$,等效的loss为
$$\begin{equation}\begin{aligned}\iint \tilde{p}(x)q(u)\bigg[ &\frac{1}{2\sigma_2^2}\Vert G(\sigma_1 u + E(x))-x\Vert^2 + \frac{1}{2}\Vert F(\sigma_1 u + E(x))\Vert^2 \\
&\quad -\log \left|\det \left[\frac{\partial F(\sigma_1 u + E(x))}{\partial u}\right]\right|\bigg] dudx\end{aligned}\end{equation}$$
而生成采样过程为
$$\begin{equation}u \sim q(u), \quad z = F^{-1}(u),\quad x = G(z)\end{equation}$$
相关 #
事实上,流模型是一大类模型的总称。除了上述以耦合层为基础的流模型(NICE、RealNVP、Glow)之外,我们还有“自回归流(autoregressive flows)”,代表作有PixelRNNs和PixelCNNs等。自回归流通常效果也不错,但是它们是逐像素地生成图片,无法并行,所以生成速度比较慢。
诸如RealNVP、Glow的流模型我们通常称为Normalizing flows(常规流),则算是另外一种流模型。尤其是Glow出来后让这类流模型再次火了一把。事实上,Glow生成图片的速度还是挺快的,就是训练周期太长了,训练成本也很大。
据我们了解,首次尝试整合VAEs和模型的是《Variational Inference with Normalizing Flows》,后面还有两个改进工作《Improving Variational Inference with Inverse Autoregressive Flow》和《Variational Lossy Autoencoder》。其实这类工作(包括本文)都是类似的。不过前面的工作都没有导出类似$\eqref{eq:f-vae-loss}$式的一般框架,而且它们都没有在图片生成上实现较大的突破。
目测我们的工作是首次将RealNVP和Glow的流模型引入到VAEs中的结果。这些“流”基于耦合层$\eqref{eq:coupling}$,容易并行计算。所以它们通常比自回归流要高效率,可以堆叠得很深。同时我们还保证隐变量维度跟输入维度一样,这个不降维的选择也能避免图像模糊问题。
实验 #
受GPU设备所限,我们仅仅在CelebA HQ上做了64x64和128x128的实验。我们先在64x64图像上对类似规模的VAEs、Glow和f-VAEs做了个对比,然后再详细展示了128x128的生成效果。
实验流程 #
首先,我们的编码器$E(\cdot)$是卷积和Squeeze算子的堆叠。具体来说,$E(\cdot)$由几个block组成,并且在每个block之前都进行一次Squeeze。而每个block由若干步复合而成,每步的形式为$x + CNN(x)$,其中$CNN(x)$是3x3和1x1的卷积组成。具体细节可以参考代码。
至于解码器(生成器)$G(\cdot)$则是卷积和UnSqueeze算子的堆叠,结构上就是$E(\cdot)$的逆。解码器的最后可以加上$\tanh (\cdot)$激活函数,但这也不是必须的。而无条件流$F(\cdot)$的结果是照搬自Glow模型,只不过没有那么深,卷积核的数目也没有那么多。
源码(基于Keras 2.2 + Tensorflow 1.8 + Python 2.7):
https://github.com/bojone/flow/blob/master/f-VAEs.py
实验结果 #
对比VAEs和f-VAEs的结果,我们可以认为f-VAEs已经基本解决了VAEs的模糊问题。对比同样规模下的Glow和f-VAEs,我们发现f-VAEs在同样的epoch下表现得更好。当然,我们不怀疑Glow在更深的时候也表现得很好甚至更好,但很明显,在同样的复杂度和同样的训练时间下,f-VAEs有着更好的表现。
f-VAEs在64x64上面的结果,只需要用GTX1060训练约120~150个epoch,大概需要7~8小时。
准确来说,f-VAEs的完整的编码器应该是$F(E(\cdot))$,即$F$和$E$的复合函数。如果在标准的流模型中,我们需要计算$E$的雅可比行列式,但是在f-VAEs中则不需要。所以$E$可以是一个普通的卷积网络,它可以实现大部分的非线性,从而简化对流模型$F$的依赖。
下面是128x128的结果(退火参数$T$指的是先验分布的标准差)。128x128的模型大概在GTX1060上训练了1.5天(约150个epoch)。
随机采样结果 #
隐变量线性插值 #
退火参数影响 #
总结 #
文章综述 #
事实上,我们这个工作的原始目标是解决针对Glow提出的两个问题:
1、如何降低Glow的计算量?
2、如何得到一个“降维”版本的Glow?
我们的结果表明,一个不降维的f-VAEs基本相当于一个迷你版本的Glow,但是能达到较好的效果。而式$\eqref{eq:f-vae-loss}$确实也允许我们训练一个降维版本的流模型。我们也从理论上证明了普通的VAEs和流模型自然地包含在我们的框架中。因此,我们的原始目标已经基本完成,得到了一个更一般的生成和推断框架。
未来工作 #
当然,我们可以看到随机生成的图片依然有一种油画的感觉。可能的原因是模型还不够复杂,但我们猜测还有一个重要原因是3x3卷积的“滥用”,导致了感知野的无限放大,使得模型无法聚焦细节。
因此,一个挑战性的任务是如何设计更好的、更合理的编码器和解码器。看起来《Network in Network》那一套会有一定的价值,还有PGGAN的结构也值得一试,但是这些都还没有验证过。
转载到请包括本文地址:https://www.spaces.ac.cn/archives/5977
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 21, 2018). 《细水长flow之f-VAEs:Glow与VAEs的联姻 》[Blog post]. Retrieved from https://www.spaces.ac.cn/archives/5977
@online{kexuefm-5977,
title={细水长flow之f-VAEs:Glow与VAEs的联姻},
author={苏剑林},
year={2018},
month={Sep},
url={\url{https://www.spaces.ac.cn/archives/5977}},
}

























December 22nd, 2022
[...]细水长flow之f-VAEs:Glow与VAEs的联姻 – 科学空间|Scientific Spaces[...]
March 10th, 2023
[...]细水长flow之f-VAEs:Glow与VAEs的联姻 - 科学空间|Scientific Spaces[...]
June 24th, 2023
[...]细水长flow之f-VAEs:Glow与VAEs的联姻 – 科学空间|Scientific Spaces[...]
November 6th, 2024
苏老师,公式(11)我想从对数密度的角度推导,却得不到正确的结果,请问是哪里的思路出现了问题吗
$$\begin{aligned}
&q_i(u)\sim\mathcal N(0,1) \quad q_i(F_x(u))\sim\mathcal{N}(\mu_i(x),\sigma_i^2(x)) \\
&q_i(u)\propto \exp(-u^2/2) \quad q_i(F_x(u)) \propto \frac{1}{\sigma_i(x)} \exp\left(\frac{(F_x(u)-\mu_i(x))^2}{-2\sigma^2_i(x)}\right)=\frac{1}{\sigma_i(x)}\exp(-1/2) \\
&\int q_i(u)\log \frac{q_i(u)}{q_i(F_x(u))}du=\mathbb E_{u\sim q_i(u)}\log \frac{q_i(u)}{q_i(F_x(u))}\\
&=\mathbb E_{u\sim q_i(u)}\left( \log \sigma_i(x)-\frac{1}{2}(u^2)+\frac{1}{2}\right)\\
&=\log \sigma_i(x) + \frac{1}{2}-\frac{1}{2}\mathbb E(u^2)\\
&=\log \sigma_i(x)
\end{aligned}$$
我看你想算的是$\mathcal N(0,1)$和$\mathcal{N}(\mu_i(x),\sigma_i^2(x))$的KL散度?这个后者不能记为$q_i(F_x(u))$,$q_i(F_x(u))$是指用$F_x(u)$替换掉$q_i(u)$中的$u$(抱歉早期的文章,记号可能有些不严谨)。
至于两个高斯分布的KL散度的计算,可以参考 https://kexue.fm/archives/5253#%E5%88%86%E5%B8%83%E6%A0%87%E5%87%86%E5%8C%96
苏老师,之前我理解$q_i(u)$和$q_i(F_x(u))$一个是关于$u$的分布,一个是关于$F_x(u)$的分布,因此不能简单套用KL散度的解析式,您的意思是$q_i(F_x(u))$应该看作$q_{Fi}(u)$直接求KL散度吗,这样的解是
$$\frac{1}{2}(\frac{1}{\sigma_i^2}+\frac{\mu_i^2}{\sigma_i^2}-1+\log \sigma^2_i)$$
也不是正确结果,不知道我哪一步想错了。
$q_i(F_x(u))$实际上是$q_i(u)|_{u\to F_x(u)}$,就是原本$q_i(u)$的概率密度函数,然后将$u$换成$F_x(u)$。
February 9th, 2025
苏老师您好,请问公式(9)中第二步的dv是如何消除的,谢谢
直接把关于$v$的积分算出来
February 9th, 2025
苏老师您好,请问隐变量经过流模型转换后,转换后的隐变量的先验分布还是正太分布吗?
是否还是标准正太分布呢,还是说会跟后验分布一样随着流模型转换变量而变化呢
“转换后的隐变量的先验分布”指啥
VAE一般不是假设隐层变量的先验分布是标准正态分布,如果隐层变量经过流模型转换后,其先验分布还是标准正态分布吗,还是说也要变成与雅可比行列式乘积后的结果
f-VAEs是降将VAE的先验分布从标准正态分布换成flow模型表达的复杂分布。
您文中(5)不是将后验分布从高斯分布转换成flow模型表达的复杂分布吗?
噢对,抱歉,是我的typo,确实是后验分布。那我理解开始的问题了。先验分布是人为指定的,这里依然是标准正态分布,就是指encoder出来后的latent再经过flow模型encode后的分布是标准正态分布。
February 28th, 2025
苏老师您好,关于最后的f-VAE章节的p(x|z),您文章中假设他服从的分布是$N(x;G(F^{-1}(z)),\sigma_2^2)$,这里如果按照前文的$z=F_x(u)$将均值化简的话结果是$N(x;G(F^{-1}F(\sigma_1u+E(x))),\sigma_2^2)=N(x;\sigma_1u+E(x),\sigma_2^2)$,这里的编码器与VAE不同,是用来输出$q(u)$分布的均值的,然后您这里通过重采样对$u\sim{N(0,I)}$进行了采样,目前看起来并没有问题。但是根据您最后给出的采样过程:$u\sim q(u),z=F^{-1}(u),x=G(z)$来看的话,这两者存在矛盾。首先您最后给出的采样过程的$F$与之前设定的似乎不一样?前文给出的$F$是将$u$映射为$z$,但是这里似乎是相反的。其次根据您采样的逻辑,以及VAE本身的流程的话,$G(*)$函数的输入应该是$z$,也就是说解码器应该输出的是$q(x|z)$分布的均值,因此前文定义的$p(x|z)=N(x;G(\sigma_1u+E(x)), \sigma_2^2)$似乎与之不匹配。这里是否应该是$q(x|z)=N(x;G(z),\sigma_2^2)=N(x;G(F_x(u)),\sigma_2^2)$。最后一个问题是$\sigma_1$和$\sigma_2$为什么是待训练的参数?首先对于$\sigma_1$来说,如果这里代表着以采样操作的话,$\sigma_1$是否应该是随机数;其次对于$\sigma_2$来说,是否应该像VAE那样设置为常数?希望苏老师能够为我解答一下,非常感谢。
抱歉现在回看起来,正文确实写得比较糟糕,这里其实没有错误,我将采样过程写成下述形式,你可能就明白了
$$z \sim q(z), \quad u = F^{-1}(z),\quad x = G(u)$$
实际上先验分布是$q(z)$,先要采样$z$,然后逆变换得到$u$,然后按照$G(u)$来生成样本。只不过我互换了一下$u,z$,显得有点难以理解。
November 12th, 2025
那公式18,是缺少了,$-\frac{1}{2} \left \| u \right \| ^{2} $.
请教一下。1,从公式15到公式18,可以不可以这样理解。在公式18中的$\frac{1}{2\sigma ^{2} } \left \| G(\sigma_{1}u +E(x) ) -x \right \| ^2 +\frac{1}{2} \left \| F(\sigma_{1}u +E(x) ) -x \right \| ^2-\frac{1}{2}\left \| u \right \| ^2 $是公式15中$-\log_{} q({F(\sigma u +x)}) $的具体展开的呢?
2,在推导公式15中,$\iint \tilde{p}(x) q(u) \log_{}{\tilde{p}(x) q(u)} \mathrm{d}u \mathrm{d}x $,这部分为什么与损失无关?
1、式$(18)$我稍微调整了一下,你再看看;
2、这一项没一个有参数的呀,对损失函数来说它就是个常数。