《方程与宇宙》:拉格朗日点的点点滴滴(四)

The New Calculation Of Lagrangian Point 1,2,3

L2_rendering

关于n体问题，选择质心或其他定点为参考点，我们可以列出下面的运动方程：
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}\tag{19}$$
现在我们只考虑三体问题。天文学家一直希望能够找到三体问题的简洁解，可是很遗憾，庞加莱已经证明了三体问题的解是混沌的，也就是说任何微小的扰动都有可能造成不可预料的后果（可以形象的比喻为：巴西的一只蝴蝶翅膀的扇动，有可能因此美国的一场龙卷风）。

三体问题演示动画：

不过，在“不和谐”中寻找“和谐”，始终是科学家的目标，因而他们瞄准了某些特解。当我们发现一个问题难以求得通解时，我们都可以尝试求一下特解，也许特解能够指引我们寻找通解之路。对于三体问题，拉格朗日寻找到了5个特解，这就是著名的拉格朗日点。

Lagrange_very_massive_svg

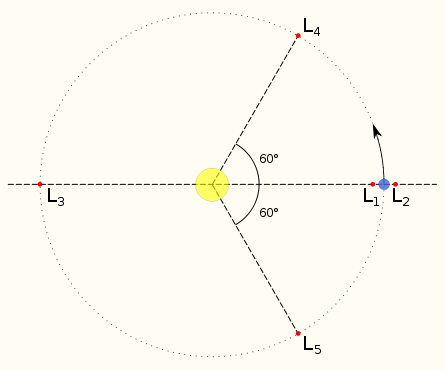
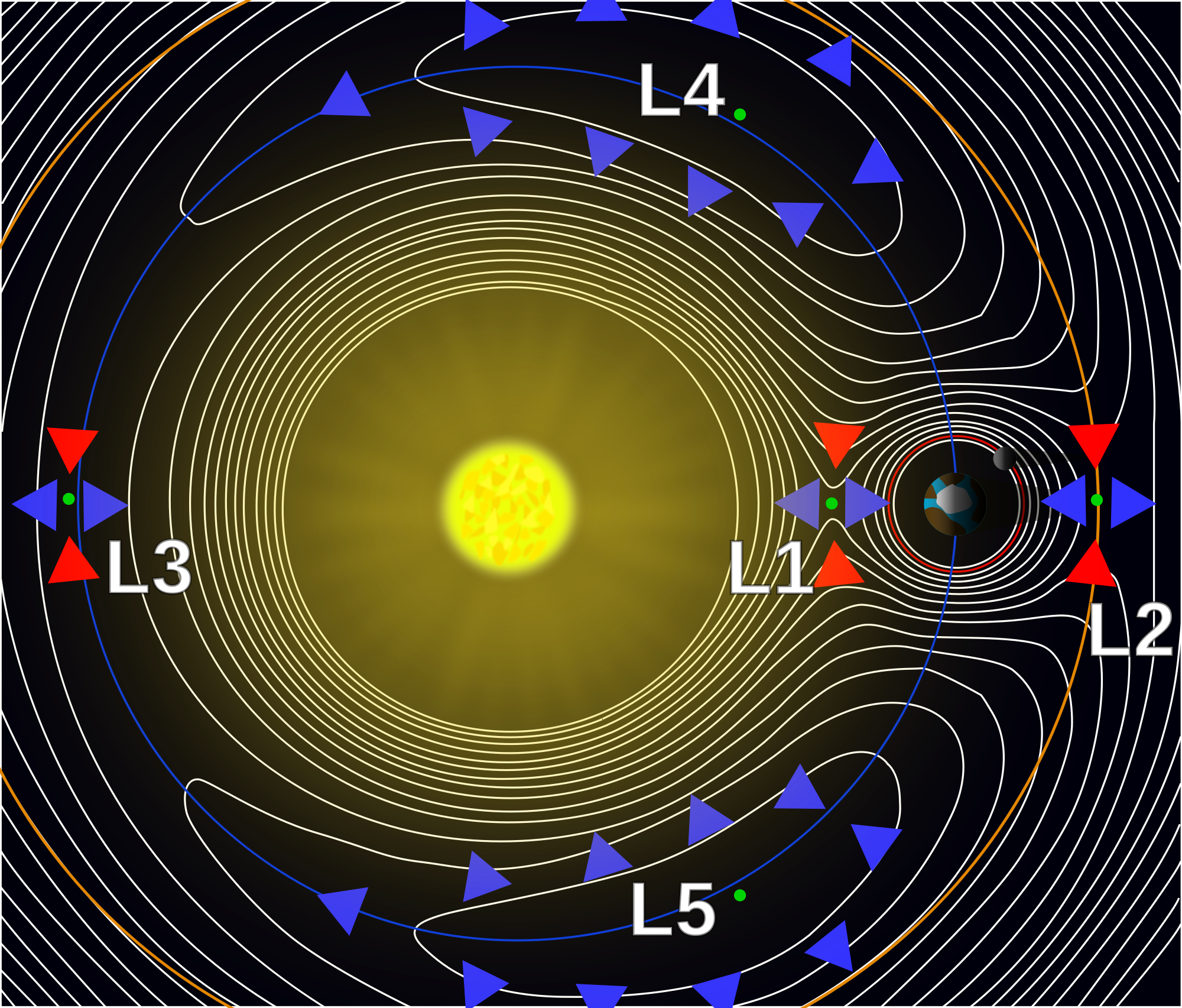
什么是拉格朗日点？拉格朗日点来源于“圆形限制性三体问题”，这个问题假设了这样一种情况：假定两个有限质量体在相互引力作用下绕其质心作圆周运动，第三个无限小质量体不对前两个天体的运动造成任何影响，只是在两个有限质量体的万有引力作用下运动。拉格朗日点就是第三个天体相对于前两个天体的位置始终保持不变的点。从下面的动画可以容易地看出这一特征：

L1：

L4_diagram_svg

换句话说，位于地球的拉格朗日点的小质量天体，它的公转周期与地球相同。根据这一特点，我们可以利用高中向心力的知识，简单地求出拉格朗日点的位置所在。因为小质量天体也在做圆周运动，它的向心力来源于太阳对它的引力与地球对它的引力的合力在向径方向的投影，所以根据向心力公式列出方程，即可以得出答案。有兴趣的读者可以自己推导，在此不详述。

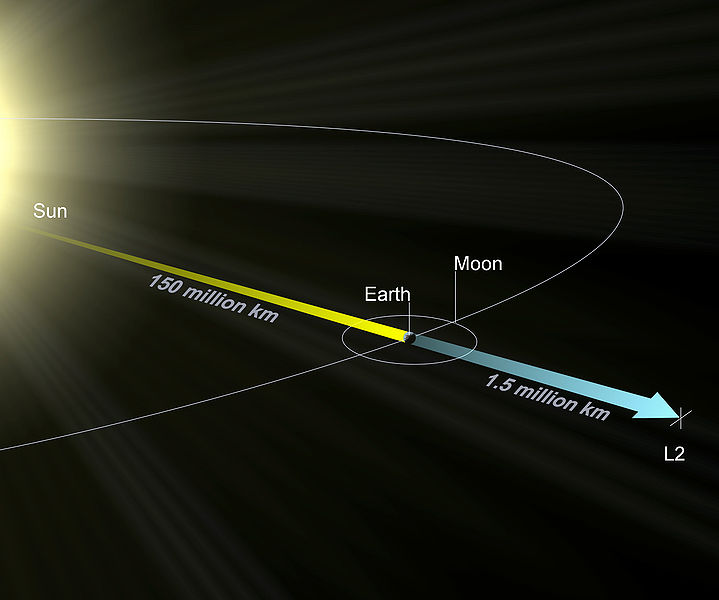
就目前来说，我们所造的一些太空探测器、人造卫星等，也有部分发射到了拉格朗日点上；受目前的科学技术所限制，飞行器的质量是可以忽略掉的。不过，圆形的三体问题始终会有一定的局限，当我们的科技发展到能够造出如月球般的探测器时，就无法忽略自身的质量了。我们希望能够得出完整的三体问题中这样的“五个特解”。这种情况下，拉格朗日点到太阳或地球的距离不再是不变的了，而是不断变化，但是比例保持不变。这个计算需要用到文章开头就给出的(1)式。我们尝试设法找出与“太阳-地球”向径共线的拉格朗日点。

拉格朗日点-推导示意图

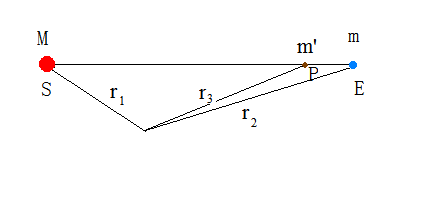
由于三者共线，我们可以设定$\vec{r}_2-\vec{r}_1=\vec{r},\vec{r}_3-\vec{r}_1=k\vec{r},|\vec{r}|=r$，太阳、地球、第三天体的质量分别为M,m,m' ，可以得出

$$\begin{aligned}\ddot{\vec{r}}_1=Gm\frac{\vec{r}_2-\vec{r}_1}{|\vec{r}_2-\vec{r}_1|^3}+Gm'\frac{\vec{r}_3-\vec{r}_1}{|\vec{r}_3-\vec{r}_1|^3}=Gm\frac{\vec{r}}{r^3}+Gm'\frac{k\vec{r}}{|k|^3 r^3} \\ \ddot{\vec{r}}_2=GM\frac{\vec{r}_1-\vec{r}_2}{|\vec{r}_1-\vec{r}_2|^3}+Gm'\frac{\vec{r}_3-\vec{r}_2}{|\vec{r}_3-\vec{r}_2|^3}=-GM\frac{\vec{r}}{r^3}-Gm'\frac{(1-k)\vec{r}}{|1-k|^3 r^3} \\ \ddot{\vec{r}}_3=GM\frac{\vec{r}_1-\vec{r}_3}{|\vec{r}_1-\vec{r}_3|^3}+Gm\frac{\vec{r}_2-\vec{r}_3}{|\vec{r}_2-\vec{r}_3|^3}=-GM\frac{k\vec{r}}{|k|^3 r^3}+Gm\frac{(1-k)\vec{r}}{|1-k|^3 r^3}\end{aligned}$$

为了化简问题，我们变换成以太阳为参照点，那么
$$\ddot{\vec{r}}=\ddot{\vec{r}}_2-\ddot{\vec{r}}_1=-G(M+m)\frac{\vec{r}}{r^3}-Gm'(\frac{1-k}{|1-k|^3}+\frac{k}{|k|^3})\frac{\vec{r}}{r^3}\tag{20}$$$$k\ddot{\vec{r}}=\ddot{\vec{r}}_3-\ddot{\vec{r}}_1=-G(M+m')\frac{k\vec{r}}{|k|^3 r^3}+Gm(\frac{1-k}{|1-k|^3}-1)\frac{\vec{r}}{r^3}\tag{21}$$
拉格朗日点要成立，必须要求(2)与(3)两个式子所表达的$\ddot{\vec{r}}$相等，因此有
$$(M+m)+m'(\frac{1-k}{|1-k|^3}+\frac{k}{|k|^3})=\frac{M+m'}{|k|^3}-m(\frac{1-k}{k|1-k|^3}-1/k)\tag{22}$$
(22)是关于k的一元五次方程，拉格朗日点即由该式给出，这只是和质量有关。由于包含绝对值，因此(22)式要分三种情况讨论，所以实际上(22)包含了3道一元五次方程。要是m'小得可以忽略的时候，(22)式可以简化成
$$M+m=\frac{M}{|k|^3}-m(\frac{1-k}{k|1-k|^3}-1/k)\tag{23}$$
将M=332918.215,m=1（太阳与地球的质量比）代入，当0< k<1时，可以求出一个实数根k=0.9900293204354188...，这就是第一拉格朗日点；当k>1时，可以求出一个实数根k=1.0100374005377246...，这就是第二拉格朗日点；当k<0时，可以求出一个实数根k=-0.9999982478231744...，这就是第三拉格朗日点。（注意，这里距离指的是拉格朗日点与太阳的距离，而非到“地日共同质心”的距离）

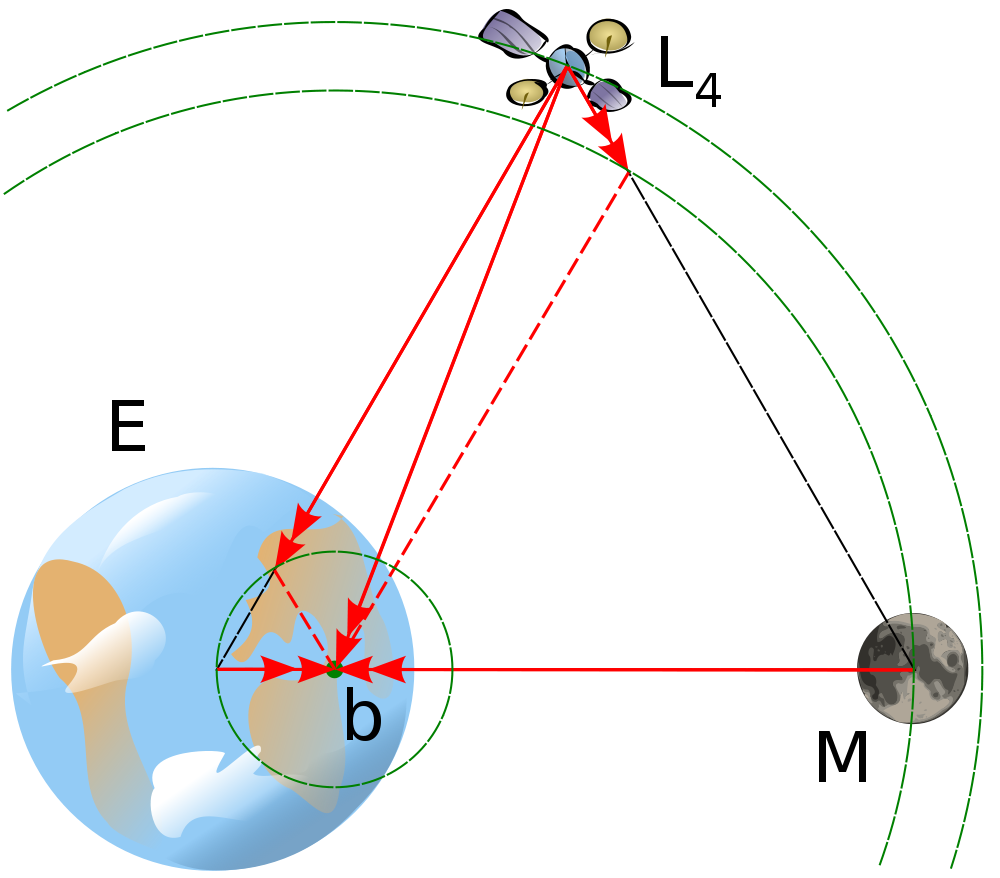
至此，我们推导出了完整的三体问题的三个拉格朗日点，这不再局限于“限制性三体问题”。当然，依旧剩下L4和L5，局限于BoJone的知识面浅薄，未能利用本文所探讨的方法给予解释，望高人指点...在推导的过程中，还让BoJone领悟到了一点：用复数可以方便地研究几何！！

剩下的L4和L5，将在下文中探讨！

洛希等势面

L2

L3

转载到请包括本文地址：https://spaces.ac.cn/archives/861

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。