从Boosting学习到神经网络：看山是山？

前段时间在潮州给韩师的同学讲文本挖掘之余，涉猎到了Boosting学习算法，并且做了一番头脑风暴，最后把Boosting学习算法的一些本质特征思考清楚了，而且得到一些意外的结果，比如说AdaBoost算法的一些理论证明也可以用来解释神经网络模型这么强大。

AdaBoost算法 #

Boosting学习，属于组合模型的范畴，当然，与其说它是一个算法，倒不如说是一种解决问题的思路。以有监督的分类问题为例，它说的是可以把弱的分类器（只要准确率严格大于随机分类器）通过某种方式组合起来，就可以得到一个很优秀的分类器（理论上准确率可以100%）。AdaBoost算法是Boosting算法的一个例子，由Schapire在1996年提出，它构造了一种Boosting学习的明确的方案，并且从理论上给出了关于错误率的证明。

以二分类问题为例子，假设我们有一批样本$\{x_i,y_i\},i=1,2,\dots,n$，其中$x_i$是样本数据，有可能是多维度的输入，$y_i\in\{1,-1\}$为样本标签，这里用1和-1来描述样本标签而不是之前惯用的1和0，只是为了后面证明上的方便，没有什么特殊的含义。接着假设我们已经有了一个弱分类器$G(x)$，比如逻辑回归、SVM、决策树等，对分类器的唯一要求是它的准确率要严格大于随机（在二分类问题中就是要严格大于0.5），所谓严格大于，就是存在一个大于0的常数$\epsilon$，每次的准确率都不低于$\frac{1}{2}+\epsilon$。

AdaBoost算法的思想是:每次用弱分类器$G(x)$训练前都为样本设置不同的权重$w_{k,1},w_{k,2},\dots,w_{k,n}$（提高之前预测错误的样本的权重），这样每次都得到不同参数的模型$G_1(x),G_2(x),\dots,G_m(x)$（当然，这里既可以是不同参数的同一个模型，又可以是多个不同模型的组合），然后通过如下的方式组合起来：
$$y=\bar{G}(x)=\text{sign}[f(x)]=\text{sign}\left[\sum_{k=1}^m \alpha_k G_k(x)\right]$$
这里$f(x)=\sum_{k=1}^m \alpha_k G_k(x)$，最后可以证明，$\bar{G}(x)$这个分类器是一个优秀的分析器。因为AdaBoost算法不是本文的重点，为了避免主次颠倒，我把具体的数学细节放到了文末。

看山是山，看水是水 #

抛开数学细节不说，我们来思考一下，AdaBoost算法究竟做了什么？或者更广泛地问，所谓组合模型，其本质是什么？

我们要做一个分类模型，通常的过程是这样的：

1、找到一批标签数据，比如文本情感分类模型中的情感评论；
2、构建特征；
3、选择适当的模型，如逻辑回归、SVM、神经网络等；
4、输入模型进行训练；
5、检验结果，优化改进。

初学者往往把精力放在第3步上面，迷恋高精度的非线性模型。事实上，精度很高的模型，往往是包含了比较强的构建特征的过程。而如果特征构建好了，即便是简单的线性模型（比如逻辑回归）都有比较高的精度。也就是说，建模的最重要一步，应该是第二步——特征的构建。

当然，构建好的特征也是最难的一步。因为构建好的特征需要对数据有着充分的认识，有时候还需要有比较专业的背景知识。如何将已有的特征组合起来，构成更好的特征，都没有统一的方法。处于这个阶段的我们，往往就是苦恼于特征的构建，并且期待着预测结果的惊喜。这也就是所谓的“看山是山，看水是水”了（看特征是特征，看结果是结果）。

看山不是山，看水不是水 #

然而，为什么不异想天开一点呢？还是假设我们有一个二元分类任务，比如文本情感分类，我们用已有的数据来训练一个模型，比如逻辑回归，得到了该模型的参数，并且输出了一些预测结果，结果的准确率高于50%。这个预测结果，难道仅仅就是结果吗？

从数学的角度来看，这个结果是通过原来的数据的线性组合，然后加上了一个逻辑函数做非线性变换得来的，说白了，是原来的特征通过某种运算得到的。仅仅看这句话，为什么不将它看成是一种构建特征的方式呢？

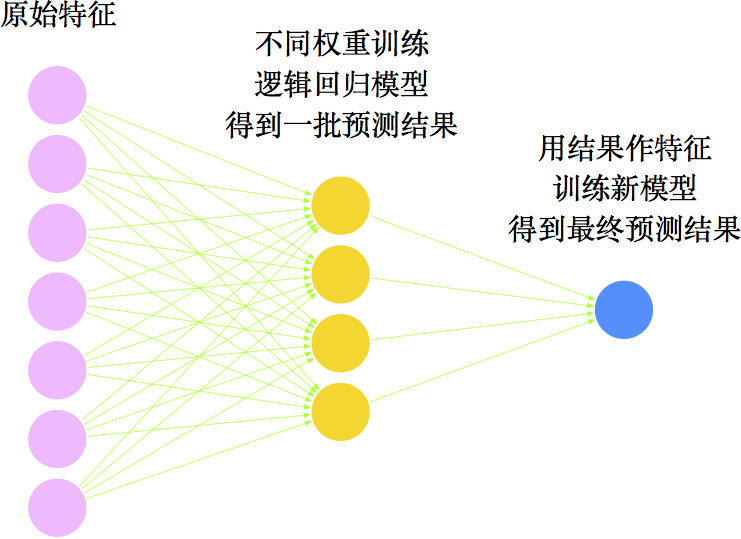
没错，它是结果，却也是特征！你用一种权重，训练出来一个逻辑回归模型，得到一批预测结果；换另外一个权重，训练另外一个不同参数的逻辑回归模型，得到一批新的预测结果；等等。为什么不把这批结果当做特征，再去一个逻辑回归模型模型呢？这个模型再不济，也不会比原来单个模型的精度差，对吧？于是乎，我们就得到了一个神奇的结论——模型既可以用来预测结果，也可以用来构建特征——结果即是特征。这时候，我们就到了“看山不是山，看水不是水”的境界了——特征与结果已经没有明显的界限了。

这时候我们也许会豁然开朗——原来Boosting学习的本质，不过就是把模型的结果视为特征，然后再做一次模型罢了。由于模型的结果基本都是不错的特征了，所以在最后一步能够把分类器的效果大大提升——特征好了，精度自然就来了。

到这里，真的想感叹一句老子的“道可道，非常道，名可名，非常名”了。

看山还是山，看水还是水 #

这是一种新的视角，把模型的结果看待为构建的一种特征。然而，我们以前就没有用过这种方法吗？

事实上是有的，可能不会很明显。假设有一个二分类问题（比如说预测是否吸烟），其中一个特征是性别，取值是男/女，那我们是怎么将它量化放进模型中的呢？我们可以用1表示男，用向量0表示女。这难道不可以看成，我们构造了如下的模型吗？
$$G(x)=\left\{\begin{aligned}&1,\quad x=\text{男}\\
&0,\quad x=\text{女}\end{aligned}\right.$$
显然，可以把它当作一个模型（这个模型的输入就是性别，输出就是是否吸烟，1表示吸烟），来预测个体是否吸烟。这本来只是表示特征的一种方法，但现在变成了一个模型的预测结果，然后我们就把这个模型的结果输入到新的模型进行预测了。回顾这个过程，不也是把结果当成了特征来输入模型了吗？

原来，我们早早用到了这种思想，只不过不够明显罢了。这时候回来思考，发现数据挖掘的很多方面都有它的影子了，也许我们已经返璞归真，有了“看山还是山，看水还是水”的感觉了。Boosting学习算法（AdaBoost算法），可以说是把这个思想发扬光大了。而看了下面的神经网络部分的描述，我们就更有这种感觉了。

神经网络 #

然而，真正将这个思想发挥到极致的，当数神经网络模型了。

神经网络模型也跟Boosting学习有关系？没错，神经网络可以看成是AdaBoost的一个特例的加强版，由此我们也可以从AdaBoost的理论证明中解释神经网络为什么这么强大。

此话怎讲？我们来回顾一下刚才说的一段话：

没错，它是结果，却也是特征！你用一种权重，训练出来一个逻辑回归模型，得到一批预测结果；换另外一个权重，训练另外一个不同参数的逻辑回归模型，得到一批新的预测结果；等等。为什么不把这批结果当做特征，再去一个逻辑回归模型模型呢？这个模型再不济，也不会比原来单个模型的精度差，对吧？

用图来表示，这是怎样的过程呢？如下图

咋看之下，这不就是一个三层的网络模型吗？

没错，这就是一个三层的神经网络模型！选择逻辑回归为弱分类器，用AdaBoost算法组合学习，结果就相当于一个三层神经网络模型！不过，神经网络还更高明一些。AdaBoost算法是逐步训练的，跟贪心算法是类似的，得到的很有可能只是局部最优解，而神经网络则把所有的参数都待定，用一个损失函数整体求最优，只要优化算法足够好，可以得到最优解。从这个角度来看，神经网络更胜一筹了。而且神经网络可以在此基础上嵌套更多层（也可以看作是以AdaBoost算法作为弱分类器，多次组合，得到更加优秀的分类器），使得效果更好。因此，在深度学习流行的今天，AdaBoost算法的意义被削弱了。不变的是，其核心思想依然具有很重要的启发意义。

不仅如此，从“将预测结果当成特征”这个角度来看，我们还可以得到RNN（递归神经网络）的结构！我们发现，目前的AdaBoost算法在最后一步构造模型之时，只用了前面的模型的输出结果作为特征，为什么不把前面的输出结果和原始数据一起作为特征来做模型呢？如果真的这样做，就构成的RNN的原型——把上一次的输出也加入到本次的输入中。

到这里，神经网络变成了AdaBoost算法的一个特例，但同时也是它的加强版，也许可以说，神经网络将组合模型的思想推到了登峰造极的地步。

此时，可谓处处皆Boosting，当真是“看山还是山，看水还是水”了！因为Boosting从来就不只是一个独立的模型，它是一种解决问题的深刻的思想——深刻的思想影响都很深远～

补充：AdaBoost算法的相关推导 #

对于AdaBoost算法，其实不难理解，但现在的难题是各个$w$和$\alpha$怎么选取？Schapire给出了一种选取方案：

1、刚开始初始化$w_{1,1}=w_{1,2}=\dots=w_{1,n}=\frac{1}{n}$，以此为权重训练得到分类器$G_1(x)$；
2、以后的每一步，按如下方式来更新$w$和$\alpha$：
$$\begin{aligned}&\alpha_k=\frac{1}{2}\log\frac{1-\varepsilon_k}{\varepsilon_k}\\
&w_{k+1,i}=\frac{1}{Z_k}w_{k,i}\exp\left(-\alpha_k y_i G_k(x_i)\right)\end{aligned}$$

其中$\varepsilon_k$是错误率，即用$G_k(x)$这个模型进行预测时，预测错误的样本数除以$n$，用数学公式写出来就是
$$\varepsilon_k = \sum_{i=1}^n w_{k,i} I\left(-y_i G_k(x_i)\right)$$
这里的$I(x)$是正计数函数
$$I(x)=\left\{\begin{aligned}&1,\quad x > 0\\
&0,\quad x\leq 0\end{aligned}\right.$$
当预测正确时，$-y_i G_k(x_i)=-1$,于是$I\left(-y_i G_k(x_i)\right)=0$，反之$I\left(-y_i G_k(x_i)\right)=1$，于是$\sum_{i=1}^n I\left(-y_i G_k(x_i)\right)$就计算了错误的个数。而$Z_k=\sum_{i=1}^n w_{k,i}\exp\left(-\alpha_k y_i G_k(x_i)\right)$是归一化因子。

最大的疑问肯定是为什么要这样选取？我也不知道Schapire是怎么想到的，也许，从错误率分析我们可以找到一些端倪。最终分类器$\bar{G}(x)$的错误率估计为
$$\begin{aligned}\varepsilon &= \frac{1}{n} \sum_{i=1}^{n} I\left(-y_i \bar{G}(x_i)\right) \\
&= \frac{1}{n} \sum_{i=1}^{n} I\left(-y_i f(x_i)\right) \\
& < \frac{1}{n} \sum_{i=1}^{n} \exp\left(-y_i f(x_i)\right)
\end{aligned}$$
其中用到了$I(x)\leq\max(0,1+x) < \max(0,e^x)=e^x$。这时候，可以代入$f$的表达式了：
$$\begin{aligned}&\frac{1}{n} \sum_{i=1}^{n} \exp(-y_i f(x_i))\\
=&\frac{1}{n}\sum_{i=1}^{n} \exp\left(-y_i \sum_{k=1}^m \alpha_k G_k (x)\right)\\
=&\frac{1}{n}\sum_{i=1}^{n} \prod_{k=1}^m\exp\left(-y_i \alpha_k G_k (x)\right)\\
=&\sum_{i=1}^{n} w_{1,i}\prod_{k=1}^m\exp\left(-y_i \alpha_k G_k (x)\right)\\
=&\sum_{i=1}^{n} w_{1,i}\exp\left(-y_i \alpha_1 G_1 (x)\right)\prod_{k=2}^m\exp\left(-y_i \alpha_k G_k (x)\right)\\
=&Z_1\sum_{i=1}^{n} w_{2,i}\prod_{k=2}^m\exp\left(-y_i \alpha_k G_k (x)\right)\\
=&\dots\\
=&Z_1 Z_2 \dots Z_m
\end{aligned}$$
回顾$Z_k$的表达式：
$$Z_k=\sum_{i=1}^n w_{k,i}\exp\left(-\alpha_k y_i G_k(x_i)\right)$$
要注意的是，$\exp\left(-\alpha_k y_i G_k(x_i)\right)$这一项看上去复杂， 但事实上它只有两种可能——$e^{-\alpha_k}$，表明预测正确；$e^{\alpha_k}$，表明预测错误，因此：
$$\begin{aligned}Z_k=&\sum_{i=1}^n w_{k,i}\exp\left(-\alpha_k y_i G_k(x_i)\right)\\
=&\sum_{\text{预测正确}} w_{k,i}e^{-\alpha_k}+\sum_{\text{预测错误}} w_{k,i}e^{\alpha_k}\\
=&e^{-\alpha_k}\sum_{\text{预测正确}} w_{k,i}+e^{\alpha_k}\sum_{\text{预测错误}} w_{k,i}\\
=&e^{-\alpha_k}(1-\varepsilon_k)+e^{\alpha_k} \varepsilon_k\\
= &2\sqrt{(1-\varepsilon_k)\varepsilon_k} \quad(\text{代入}\alpha_k=\frac{1}{2}\log\frac{1-\varepsilon_k}{\varepsilon_k}\text{即得})\\
=&\sqrt{1-4\gamma_k^2}\quad (\text{记}\gamma_k = \frac{1}{2}-\varepsilon_k)\\
\leq&\exp\left(-2\gamma_k^2\right)
\end{aligned}$$
所以
$$\varepsilon < Z_1 Z_2 \dots Z_m < \exp\left(-2\sum_{k=1}^m \gamma_k^2\right)$$
如果$\gamma_k$有正的下界（这也就是为什么弱分类器的正确率要严格大于随机），那么错误率将是趋于0的，而且是指数下降，这是非常理想的。当然，即便这样的出来一个准确率100%的模型，一般也只能在数据内部使用，换言之，很可能出现过拟合现象，不过，这应该是很极端的情况了，事实上AdaBoost的过拟合现象并不严重。

关于Boosting算法，我就不进一步举例子了，更多内容可以参考：
http://www.52caml.com/head_first_ml/ml-chapter6-boosting-family/

转载到请包括本文地址：https://spaces.ac.cn/archives/3873

更详细的转载事宜请参考：《科学空间FAQ》