Seq2Seq中Exposure Bias现象的浅析与对策
By 苏剑林 | 2020-03-09 | 113467位读者 |前些天笔者写了《CRF用过了,不妨再了解下更快的MEMM?》,里边提到了MEMM的局部归一化和CRF的全局归一化的优劣。同时,笔者联想到了Seq2Seq模型,因为Seq2Seq模型的典型训练方案Teacher Forcing就是一个局部归一化模型,所以它也存在着局部归一化所带来的毛病——也就是我们经常说的“Exposure Bias”。带着这个想法,笔者继续思考了一翻,将最后的思考结果记录在此文。
本文算是一篇进阶文章,适合对Seq2Seq模型已经有一定的了解、希望进一步提升模型的理解或表现的读者。关于Seq2Seq的入门文章,可以阅读旧作《玩转Keras之seq2seq自动生成标题》和《从语言模型到Seq2Seq:Transformer如戏,全靠Mask》。
本文的内容大致为:
1、Exposure Bias的成因分析及例子;
2、简单可行的缓解Exposure Bias问题的策略。
Softmax #
首先,我们来回顾Softmax相关内容。大家都知道,对于向量$(x_1,x_2,\dots,x_n)$,它的Softmax为
\begin{equation}(p_1,p_2,\dots,p_n)=\frac{1}{\sum\limits_{i=1}^n e^{x_i}}\left(e^{x_1},e^{x_2},\dots,e^{x_n}\right)\end{equation}
由于$e^t$是关于$t$的严格单调递增函数,所以如果$x_k$是$x_1,x_2,\dots,x_n$中的最大者,那么$p_k$也是$p_1,p_2,\dots,p_n$中的最大者。
对于分类问题,我们所用的loss一般是交叉熵,也就是
\begin{equation}-\log p_t = \log\left(\sum\limits_{i=1}^n e^{x_i}\right) - x_t\end{equation}
其中$t$是目标类。如文章《寻求一个光滑的最大值函数》所述,上式第一项实际上是$\max\left(x_1,x_2,\dots,x_n\right)$的光滑近似,所以为了形象理解交叉熵,我们可以写出
\begin{equation}-\log p_t \approx \max\left(x_1,x_2,\dots,x_n\right) - x_t\end{equation}
也就是说,交叉熵实际上在缩小目标类得分$x_t$与全局最大值的差距,显然这个差距最小只能为0,并且此时目标类得分就是最大值者。所以,Softmax加交叉熵的效果就是“希望目标类的得分成为最大值”。
Teacher Forcing #
现在,我们来看Seq2Seq,它通过条件分解来建模联合概率分布:
\begin{equation}\begin{aligned}p(\boldsymbol{y}|\boldsymbol{x})=&\,p(y_1,y_2,\dots,y_n|\boldsymbol{x})\\
=&\,p(y_1|\boldsymbol{x})p(y_2|\boldsymbol{x},y_1)\dots p(y_n|\boldsymbol{x},y_1,\dots,y_{n-1})
\end{aligned}\end{equation}
每一项自然也就用Softmax来建模的,即
\begin{equation}\begin{aligned}&p(y_1|\boldsymbol{x})=\frac{e^{f(y_1;\boldsymbol{x})}}{\sum\limits_{y_1}e^{f(y_1;\boldsymbol{x})}},\\
&p(y_2|\boldsymbol{x},y_1)=\frac{e^{f(y_1,y_2;\boldsymbol{x})}}{\sum\limits_{y_2}e^{f(y_1,y_2;\boldsymbol{x})}},\\
&\dots,\\
&p(y_n|\boldsymbol{x},y_1,\dots,y_{n-1})=\frac{e^{f(y_1,y_2,\dots,y_n;\boldsymbol{x})}}{\sum\limits_{y_n}e^{f(y_1,y_2,\dots,y_n;\boldsymbol{x})}}
\end{aligned}\end{equation}
乘起来就是
\begin{equation}p(\boldsymbol{y}|\boldsymbol{x})=\frac{e^{f(y_1;\boldsymbol{x})+f(y_1,y_2;\boldsymbol{x})+\dots+f(y_1,y_2,\dots,y_n;\boldsymbol{x})}}{\left(\sum\limits_{y_1}e^{f(y_1;\boldsymbol{x})}\right)\left(\sum\limits_{y_2}e^{f(y_1,y_2;\boldsymbol{x})}\right)\dots\left(\sum\limits_{y_n}e^{f(y_1,y_2,\dots,y_n;\boldsymbol{x})}\right)}\label{eq:join-target}\end{equation}
而训练目标就是
\begin{equation}-\log p(\boldsymbol{y}|\boldsymbol{x})=-\log p(y_1|\boldsymbol{x})-\log p(y_2|\boldsymbol{x},y_1)-\dots -\log p(y_n|\boldsymbol{x},y_1,\dots,y_{n-1})\end{equation}
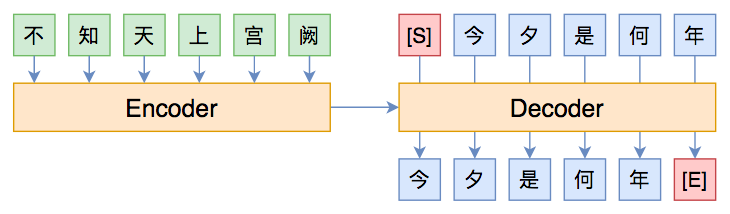
这个直接的训练目标就叫做Teacher Forcing,因为在算$-\log p(y_2|\boldsymbol{x},y_1)$的时候我们要知道真实的$y_1$,在算$-\log p(y_3|\boldsymbol{x},y_1,y_2)$我们需要知道真实的$y_1,y_2$,依此类推,这就好像有一个经验丰富的老师预先给我们铺好了大部分的路,让我们只需要求下一步即可。这种方法训练起来简单,而且结合CNN或Transformer那样的模型就可以实现并行的训练,但它可能会带来Exposure Bias问题。
Exposure Bias #
其实Teacher Forcing这个名称本身就意味着它本身会存在Exposure Bias问题。回想一下老师教学生解题的过程,一般的步骤为:
1、第一步应该怎么思考;
2、第一步想出来后,第二步我们有哪些选择;
3、确定了第二步后,第三步我们可以怎么做;
...
n、有了这n-1步后,最后一步就不难想到了。
这个过程其实跟Seq2Seq的Teacher Forcing方案的假设是一样的。有过教学经验的读者就知道,通常来说学生们都能听得频频点头,感觉全都懂了,然后让学生课后自己做题,多数还是一脸懵比。为什么会这样呢?其中一个原因就是Exposure Bias。说白了,问题就在于,老师总是假设学生能想到前面若干步后,然后教学生下一步,但如果前面有一步想错了或者想不出来呢?这时候这个过程就无法进行下去了,也就是没法得到正确答案了,这就是Exposure Bias问题。
Beam Search #
事实上,我们真正做题的时候并不总是这样子,假如我们卡在某步无法确定时,我们就遍历几种选择,然后继续推下去,看后面的结果反过来辅助我们确定前面无法确定的那步。对应到Seq2Seq来说,这其实就相当于基于Beam Search的解码过程。
对于Beam Search,我们应该能发现,beam size并不是越大越好,有些情况甚至是beam size等于1时最好,这看起来有点不合理,因为beam size越大,理论上找到的序列就越接近最优序列,所以应该越有可能正确才对。事实上这也算是Exposure Bias的现象之一。
从式$\eqref{eq:join-target}$我们可以看出,Seq2Seq对目标序列$y_1,y_2,\dots,y_n$的打分函数为:
\begin{equation}f(y_1;\boldsymbol{x})+f(y_1,y_2;\boldsymbol{x})+\dots+f(y_1,y_2,\dots,y_n;\boldsymbol{x})\end{equation}
正常来说,我们希望目标序列是所有候选序列之中分数最高的,根据本文开头介绍的Softmax方法,我们建立的概率分布应该是
\begin{equation}p(\boldsymbol{y}|\boldsymbol{x})=\frac{e^{f(y_1;\boldsymbol{x})+f(y_1,y_2;\boldsymbol{x})+\dots+f(y_1,y_2,\dots,y_n;\boldsymbol{x})}}{\sum\limits_{y_1,y_2,\dots,y_n}e^{f(y_1;\boldsymbol{x})+f(y_1,y_2;\boldsymbol{x})+\dots+f(y_1,y_2,\dots,y_n;\boldsymbol{x})}}\label{eq:ideal-target}\end{equation}
但上式的分母需要遍历所有路径求和,难以实现,而式$\eqref{eq:join-target}$就作为一种折衷的选择得到了广泛应用。但式$\eqref{eq:join-target}$跟式$\eqref{eq:ideal-target}$并不等价,因此哪怕模型已经成功优化,也可能出现“最优序列并不是目标序列”的现象。
简单例子 #
我们来举一个简单例子。设序列长度只有2,候选序列是$(a,b)$和$(c,d)$,而目标序列是$(a,b)$,训练完成后,模型的概率分布情况为
$$\begin{array}{c|c}
\hline
p(a) & p(c)\\
\hline
0.6 & 0.4 \\
\hline
\end{array}\qquad \begin{array}{c|c|c|c}
\hline
p(b|a) & p(d|a) & p(b|c) & p(d|c)\\
\hline
0.55 & 0.45 & 0.1 & 0.9\\
\hline
\end{array}$$
如果beam size为1,那么因为$p(a) > p(c)$,所以第一步只能输出$a$,接着因为$p(b|a) > p(d|a)$,所以第二步只能输出$b$,成功输出了正确序列$(a,b)$。但如果beam size为2,那么第一步输出$(a,0.6),(c,0.4)$,而第二步遍历所有组合,我们得到
\begin{array}{c|c|c|c}
\hline
(a, b) & (a, d) & (c, b) & (c, d)\\
\hline
0.33 & 0.27 & 0.04 & 0.36\\
\hline
\end{array}
所以输出了错误的序列$(c,d)$。
那是因为模型没训练好吗?并不是,前面说过Softmax加交叉熵的目的就是让目标的得分最大,对于第一步我们有$p(a) > p(c)$,所以第一步的训练目标已经达到了,而第二步在$a$已经预先知道的前提下我们有$p(b|a) > p(d|a)$,这说明第二步的训练目标也达到了。因此,模型已经算是训练好了,只不过可能因为模型表达能力限制等原因,得分并没有特别高,但“让目标的得分最大”这个目标已经完成了。
思考对策 #
从上述例子中读者或许可以看出问题所在了:主要是$p(d|c)$太高了,而$p(d|c)$是没有经过训练的,没有任何显式的机制去抑制$p(d|c)$变大,因此就出现了“最优序列并不是目标序列”的现象。
看到这里,读者可能就能想到一个朴素的对策了:添加额外的优化目标,降低那些Beam Search出来的非目标序列不就行了?事实上,这的确是一个有效的解决方法,相关结果发表在2016年的论文《Sequence-to-Sequence Learning as Beam-Search Optimization》。但这样一来几乎要求每步训练前的每个样本都要进行一次Beam Search,计算成本太大。还有一些更新的结果,比如ACL 2019的最佳长论文《Bridging the Gap between Training and Inference for Neural Machine Translation》就是聚焦于解决Exposure Bias问题。此外,通过强化学习直接优化BLEU等方法,也能一定程度上缓解Exposure Bias。
然而,据笔者所了解,这些致力于解决Exposure Bias的方法,大部分都是大刀阔斧地改动了训练过程,甚至会牺牲原来模型的训练并行性(需要递归地采样负样本,如果模型本身是RNN那倒无妨,但如果本身是CNN或Transformer,那伤害就很大了),成本的提升幅度比效果的提升幅度大得多。
构建负样本 #
纵观大部分解决Exposure Bias的论文,以及结合我们前面的例子和体会,不难想到,其主要思想就是构造有代表性的负样本,然后在训练过程中降低这些负样本的概率,所以问题就是如何构造“有代表性”的负样本了。这里给出笔者构思的一种简单策略,实验证明它能一定程度上缓解Exposure Bias,提升文本生成的表现,重要的是,这种策略比较简单,基本能做到即插即用,几乎不损失训练性能。
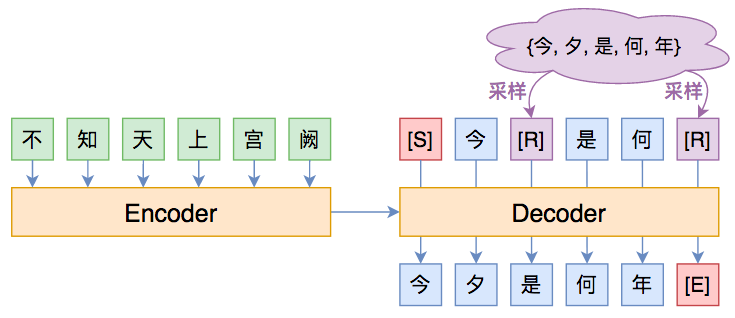
方法很简单,就是随机替换一下Decoder的输入词(Decoder的输入词有个专门的名字,叫做oracle words),如下图所示:
其中紫色的[R]代表被随机替换的词。其实不少Exposure Bias的论文也是这个思路,只不过随机选词的方案不一样。笔者提出的方案很简单:
1、50%的概率不做改变;
2、50%的概率把输入序列中30%的词替换掉,替换对象为原目标序列的任意一个词。
也就是说,随机替换发生概率是50%,随机替换的比例是30%,随机抽取空间就是目标序列的词集。这个策略的灵感在于:尽管Seq2Seq不一定能完全生成目标序列,但它通常能生成大部分目标序列的词(但顺序可能不对,或者重复出现同一些词),因此这样替换后的输入序列通常可以作为有代表性的负样本。对了,说明一下,50%和30%这两个比例纯粹是拍脑袋的,没仔细调参,因为生成模型调一次实在是太累了。
效果如何呢?笔者做了两个标题(摘要)生成的实验(就是CLGE的前两个),其中baseline是task_seq2seq_autotitle_csl.py,代码开源于:
结果如下表:
\begin{array}{c}
\text{CSL标题生成实验结果}\\
{\begin{array}{c|c|cccc}
\hline
& \text{beam size} & \text{Rouge-L} & \text{Rouge-1} & \text{Rouge-2} & \text{BLEU} \\
\hline
\text{baseline} & 1 & 63.81 & 65.45 & 54.91 & 45.52 \\
\text{随机替换} & 1 & \textbf{64.44} & \textbf{66.09} & \textbf{55.56} & \textbf{46.1} \\
\hline
\text{baseline} & 2 & 64.44 & 66.09 & 55.75 & 46.39 \\
\text{随机替换} & 2 & \textbf{65.04} & \textbf{66.75} & \textbf{56.51} & \textbf{47.19} \\
\hline
\text{baseline} & 3 & 64.75 & 66.34 & 56.06 & 46.7 \\
\text{随机替换} & 3 & \textbf{65.15} & \textbf{66.96} & \textbf{56.74} & \textbf{47.42} \\
\hline
\end{array}}\\
\\
\text{LCSTS摘要生成实验结果}\\
{\begin{array}{c|c|cccc}
\hline
& \text{beam size} & \text{Rouge-L} & \text{Rouge-1} & \text{Rouge-2} & \text{BLEU} \\
\hline
\text{baseline} & 1 & 27.99 & 29.57 & \textbf{18.04} & \textbf{11.72} \\
\text{随机替换} & 1 & \textbf{28.61} & \textbf{29.92} & 17.72 & 11.23 \\
\hline
\text{baseline} & 2 & \textbf{29.2} & 30.7 & \textbf{19.17} & \textbf{12.64} \\
\text{随机替换} & 2 & 29.15 & \textbf{30.79} & 18.56 & 11.75 \\
\hline
\text{baseline} & 3 & \textbf{29.45} & \textbf{30.95} & \textbf{19.5} & \textbf{12.93} \\
\text{随机替换} & 3 & 29.14 & 30.88 & 18.76 & 11.91 \\
\hline
\end{array}}
\end{array}
可以发现,在CSL任务中,基于随机替换的策略稳定提升了文本生成的所有指标,而LCSTS任务的各个指标则各有优劣,考虑到LCSTS本身比较难,各项指标本来就低,所以应该说CSL的结果更有说服力一些。这表明,笔者提出的上述策略确实是一种值得尝试的方案。(注:所有实验都重复了两次然后取平均,所以实验结果应该是比较可靠的了。)
对抗训练 #
思考到这里,我们不妨再“天马行空”一下:既然解决Exposure Bias的思路之一就是要构造有代表性的负样本输入,说白了就是让模型在扰动下依然能预测正确,而前些天我们不是才讨论了一种生成扰动样本的方法吗?不错,那就是对抗训练。如果直接往baseline模型里边加入对抗训练,能不能提升模型的性能呢?简单起见,笔者做了往baseline模型里边梯度惩罚(也算是对抗训练的一种)的实验,结果对比如下:
\begin{array}{c}
\text{CSL标题生成实验结果}\\
{\begin{array}{c|c|cccc}
\hline
& \text{beam size} & \text{Rouge-L} & \text{Rouge-1} & \text{Rouge-2} & \text{BLEU} \\
\hline
\text{baseline} & 1 & 63.81 & 65.45 & 54.91 & 45.52 \\
\text{随机替换} & 1 & 64.44 & 66.09 & 55.56 & 46.1 \\
\text{梯度惩罚} & 1 & \textbf{65.41} & \textbf{67.29} & \textbf{56.64} & \textbf{47.37} \\
\hline
\text{baseline} & 2 & 64.44 & 66.09 & 55.75 & 46.39 \\
\text{随机替换} & 2 & 65.04 & 66.75 & 56.51 & 47.19 \\
\text{梯度惩罚} & 2 & \textbf{65.94} & \textbf{67.84} & \textbf{57.38} & \textbf{48.16} \\
\hline
\text{baseline} & 3 & 64.75 & 66.34 & 56.06 & 46.7 \\
\text{随机替换} & 3 & 65.15 & 66.96 & 56.74 & 47.42 \\
\text{梯度惩罚} & 3 & \textbf{66.1} & \textbf{68.08} & \textbf{57.7} & \textbf{48.56} \\
\hline
\end{array}}\\
\\
\text{LCSTS摘要生成实验结果}\\
{\begin{array}{c|c|cccc}
\hline
& \text{beam size} & \text{Rouge-L} & \text{Rouge-1} & \text{Rouge-2} & \text{BLEU} \\
\hline
\text{baseline} & 1 & 27.99 & 29.57 & 18.04 & 11.72 \\
\text{随机替换} & 1 & 28.61 & 29.92 & 17.72 & 11.23 \\
\text{梯度惩罚} & 1 & \textbf{30.75} & \textbf{31.83} & \textbf{19.38} & \textbf{11.78} \\
\hline
\text{baseline} & 2 & 29.2 & 30.7 & 19.17 & \textbf{12.64} \\
\text{随机替换} & 2 & 29.15 & 30.79 & 18.56 & 11.75 \\
\text{梯度惩罚} & 2 & \textbf{30.88} & \textbf{32.19} & \textbf{19.96} & 12.32 \\
\hline
\text{baseline} & 3 & 29.45 & 30.95 & 19.5 & \textbf{12.93} \\
\text{随机替换} & 3 & 29.14 & 30.88 & 18.76 & 11.91 \\
\text{梯度惩罚} & 3 & \textbf{30.39} & \textbf{31.76} & \textbf{19.74} & 12.14 \\
\hline
\end{array}}
\end{array}
可以看到,对抗训练(梯度惩罚)进一步提升了CSL生成的所有指标,而LCSTS上主要提升的是Roune指标,BLEU则有所下降。因此,对抗训练也可以列入“提升文本生成模型的潜力技巧”名单之中。
本文小结 #
本文讨论了Seq2Seq中的Exposure Bias现象,尝试从直观上和理论上分析Exposure Bias的原因,并给出了简单可行的缓解Exposure Bias问题的对策,其中包括笔者构思的一种随机替换策略,以及基于对抗训练的策略,这两种策略的好处是它们几乎是即插即用的,并且实验表明它们能一定程度上提升文本生成的各个指标。
转载到请包括本文地址:https://www.spaces.ac.cn/archives/7259
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 09, 2020). 《Seq2Seq中Exposure Bias现象的浅析与对策 》[Blog post]. Retrieved from https://www.spaces.ac.cn/archives/7259
@online{kexuefm-7259,
title={Seq2Seq中Exposure Bias现象的浅析与对策},
author={苏剑林},
year={2020},
month={Mar},
url={\url{https://www.spaces.ac.cn/archives/7259}},
}










March 9th, 2020
你好,task_seq2seq_autotitle_csl.py代码中好像没看到相关的代码?
我没说task_seq2seq_autotitle_csl.py有相关代码啊...
算了算了,还是开源吧:https://github.com/bojone/exposure_bias
March 9th, 2020
苏神好,最近也在研究这个。ICLR2020有一篇paper叫Calibration, Entropy Rates, and Memory in Language Models
感觉正好也是解决这个问题的。只是里面一些针对概率的操作不是很理解,不知道苏神有没有时间解读一下?
谢谢推荐,我先读读~
好的,非常感谢!
粗略看了下,好像好专业的样子...先搁着了(捂脸)
March 10th, 2020
"而第二步假设a已经知道的前提下我们有p(b|a)>p(c|a)" 中应该是p(b|a)>p(d|a) 吧
是的,感谢你的认真阅读,已经更正。
March 10th, 2020
类似于跟bert中的概率mask\替换 是吧?
有点类似,但不是替换为[MASK],是替换为序列中的任意一个词
March 10th, 2020
之前在读 Bridging the Gap between Training and Inference for Neural Machine Translation 这个文章的时候就好奇里面介绍生成oracle words的方案都是以牺牲并行性为代价的,是不是值得. 然后自己实现了一个类似的方案就是在decoder部分的logits上的top_k按照的归一化概率随机选择oracle words, 并且借鉴了文章里面sampling with decay的技巧, 避免模型学"歪"了. 不过看到随机替换效果也不错, 看来又可以减少点儿计算量了
这篇论文里边模型的主体结构就是RNN吧,所以他们的改进对RNN来说算不上牺牲并行性。
March 10th, 2020
苏神,能简单说下为什么构建负样本就能缓解Exposure Bias,可以举个例子吗?
比如本文的那个小例子,如果构造了负样本$(c,d)$,那么让decoder的输入为$(c,d)$,输出为$(a,b)$,那么$p(d|c)$就不会那么高了(因为这时候模型会有倾向地提高$p(b|c)$,等价于降低了$p(d|c)$),从而不会再输出错误解码$(c,d)$。
首先感谢苏神的分享。假设目标序列是 $(a,b)$,按照上面构造负样本的策略,应该不能直接构造出$(c,d)$哈?扩大随机替换的空间也许有进一步的提升空间?例如用同义词替换或模型译文的词集进行替换。
根据本文的策略是不能直接从$(a,b)$构建出$(c,d)$。但是其实这个例子比较极端,而实际情况下,高频的负样本跟正样本之间往往有大量重合之处,本文的策略正是基于这一点构思的。
March 12th, 2020
苏神好,简单例子里的beam size为2,第一步输出(a, 0.6),(b, 0.4),其实是(a, 0.6),(c, 0.4)吗?
对对对,谢谢指出,已经修正。
March 13th, 2020
主要原因是seq2seq建模$p(y_{1},y_{2},y_{3}|\mathbf{x})$的时候不满足能量模型,相反他把每个condition distribution建模成了能量模型。
这是现象,不能算原因吧?因为还需要回答“为什么不满足能量模型就不够好”。
是的,能量模型具有最大熵的形式,这就是他优越的地方
这只不过换了个名字,依然只是现象而不是原因...
为什么具有最大熵的形式就更好?
March 15th, 2020
苏神,我接触NLP有半年的时间了。我这两天正在进行一个关系抽取的比赛,不知道苏神是否有时间可以分享一下自己如何评价一个模型是好是坏,或者好在哪?坏在哪?
比如一个模型如果效果不好,该怎么寻找效果差的原因。
虽然我知道神经网络是科学,不是玄学,但我始终get不到如何对一个模型进行科学的评测或调整。现阶段,我对模型进行设计基本就是属于互拼乱凑,不讲究方法,又或者是借鉴别人的结构,但是自己却不会更改。
苏神可否分享一下其中的“方法”?又或者说在神经网络这一领域,有没有什么常识可言?
谢谢苏神!
观察bad case,思考对策。
好的。谢谢苏神
September 29th, 2020
hi,又来学习了!发现一个奇怪的地方,在Softmax章节最后一段,(1)“显然这个差距最小只能为o”->(2)“显然这个差距最小只能为0”。 在文中目测是 'o',但是粘贴下来,发现是'0'。还以为是笔误,看来可能是排版问题?
啥意思?我复制下来的结果就是“零”而不是“欧”呀,而我要表达的意思就是“零”啊。
复制下来是'零',但是看着像'欧'