又是Dropout两次！这次它做到了有监督任务的SOTA

关注NLP新进展的读者，想必对四月份发布的SimCSE印象颇深，它通过简单的“Dropout两次”来构造正样本进行对比学习，达到了无监督语义相似度任务的全面SOTA。无独有偶，最近的论文《R-Drop: Regularized Dropout for Neural Networks》提出了R-Drop，它将“Dropout两次”的思想用到了有监督任务中，每个实验结果几乎都取得了明显的提升。此外，笔者在自己的实验还发现，它在半监督任务上也能有不俗的表现。

小小的“Dropout两次”，居然跑出了“五项全能”的感觉，不得不令人惊讶。本文来介绍一下R-Drop，并分享一下笔者对它背后原理的思考。

SimCSE #

《中文任务还是SOTA吗？我们给SimCSE补充了一些实验》中，我们已经对SimCSE进行了介绍。简单来说，SimCSE是NLP的一种对比学习方案，对比学习的标准流程是同一个样本通过不同的数据扩增手段得到的结果视为正样本对，而batch内的所有其他样本视为负样本，然后就是通过loss来缩小正样本的距离、拉大负样本的距离了。

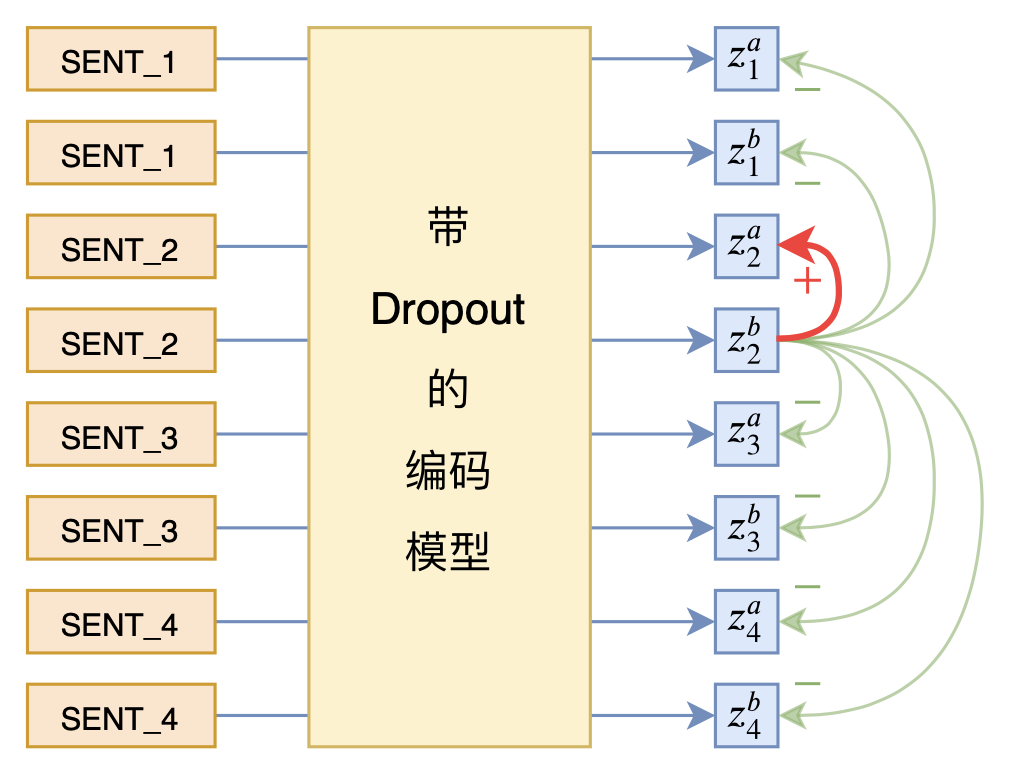
所以难度主要集中在数据扩增手段上。对于NLP来说，我们很难人工构建保证语义不变的数据扩增，所以SimCSE干脆不人工进行数据扩增，而是通过“Dropout两次”的方式来得到同一个输入的不同特征向量，并将它们视为正样本对。奇怪的是，这个简单的“Dropout两次”构造正样本，看上去是一种“无可奈何”的妥协选择，但消融实验却发现它几乎优于所有其他数据扩增方法，令人惊讶之余又让人感叹“大道至简”。

SimCSE示意图

在实现上，SimCSE也相当简单，所谓“Dropout两次”，只需要将样本重复地输入到模型，然后计算相应的loss就行了，如上图所示。由于Dropout本身的随机性，每个样本的Dropout模式都是不一样的，所以只要单纯地重复样本，就可以实现“Dropout两次”的效果。

R-Drop #

从结果上来看，SimCSE就是希望Dropout对模型结果不会有太大影响，也就是模型输出对Dropout是鲁棒的。所以很明显，“Dropout两次”这种思想是可以推广到一般任务的，这就是R-Drop（Regularized Dropout）。

分类问题 #

在笔者看来，R-Drop跟SimCSE是高度相关的，甚至R-Drop应该是受到了SimCSE启发的，不过R-Drop论文并没有引用SimCSE，所以这就比较迷了。

R-Drop示意图

具体来说，以分类问题为例，训练数据为$\{x_i,y_i\}_{i=1}^n$，模型为$P_{\theta}(y|x)$，每个样本的loss一般是交叉熵
\begin{equation}\mathcal{L}_i = -\log P_{\theta}(y_i|x_i)\end{equation}
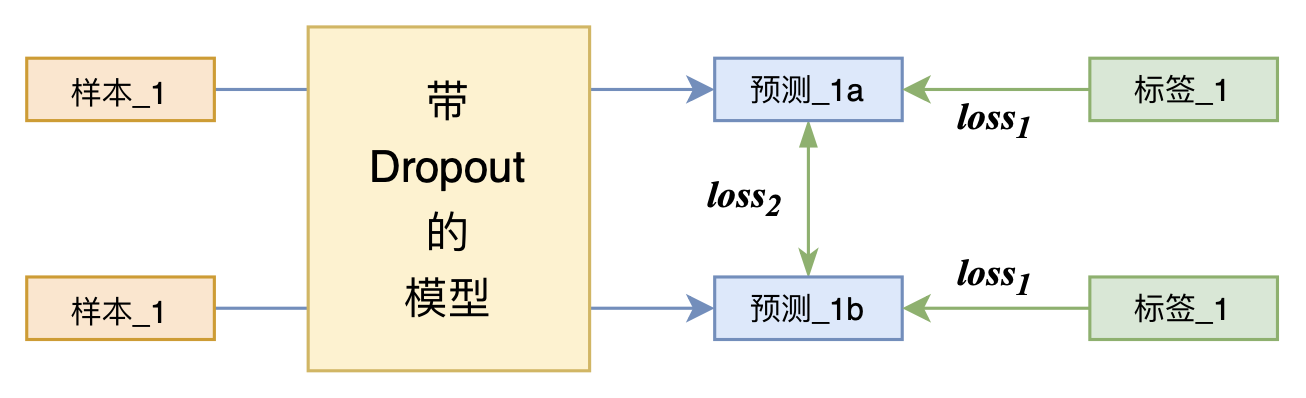
在“Dropout两次”的情况下，其实我们可以认为样本已经通过了两个略有不同的模型，我们分别记为$P_{\theta}^{(1)}(y|x)$和$P_{\theta}^{(2)}(y|x)$。这时候R-Drop的loss分为两部分，一部分是常规的交叉熵：
\begin{equation}\mathcal{L}_i^{(CE)} = -\log P_{\theta}^{(1)}(y_i|x_i) -\log P_{\theta}^{(2)}(y_i|x_i)\label{eq:ce}\end{equation}
另一部分则是两个模型之间的对称KL散度，它希望不同Dropout的模型输出尽可能一致：
\begin{equation}\mathcal{L}_i^{(KL)} = \frac{1}{2}\big[KL\left(P_{\theta}^{(2)}(y|x_i)\big\Vert P_{\theta}^{(1)}(y|x_i)\right) + KL\left(P_{\theta}^{(1)}(y|x_i)\big\Vert P_{\theta}^{(2)}(y|x_i)\right)\big]\label{eq:kl}\end{equation}
最终loss就是两个loss的加权和：
\begin{equation}\mathcal{L}_i = \mathcal{L}_i^{(CE)} + \alpha\mathcal{L}_i^{(KL)}\end{equation}
也就是说，它在常规交叉熵的基础上，加了一项强化模型鲁棒性正则项。

一般形式 #

可能有些读者会问非分类问题应该将$KL$项替换为什么，事实上原论文并没有在非分类问题上进行实验，不过这里可以补充一下。我们可以留意到
\begin{equation}-\log P_{\theta}(y_i|x_i) = KL\left(\text{one_hot}(y_i)\big\Vert P_{\theta}(y|x_i)\right)\end{equation}
所以，上述$\mathcal{L}_i$只不过是$KL$散度的反复使用，它的一般形式是：
\begin{equation}\mathcal{L}_i = \mathcal{D}\left(y_i, f_{\theta}^{(1)}(x_i)\right)+\mathcal{D}\left(y_i, f_{\theta}^{(2)}(x_i)\right) + \frac{\alpha}{2} \left[\mathcal{D}\left(f_{\theta}^{(2)}(x_i), f_{\theta}^{(1)}(x_i)\right)+\mathcal{D}\left(f_{\theta}^{(1)}(x_i), f_{\theta}^{(2)}(x_i)\right)\right]\end{equation}
因此对于非分类问题，我们将$\mathcal{D}$换成适当的度量（而不是$KL$散度）即可。

实验效果 #

我们先来看看R-Drop的实验结果。

R-Drop的主要超参有三个：batch_size、$\alpha$和Dropout概率。batch_size一般取决于我们的算力，对个人来说调整空间不大；原论文的$\alpha$从$1\sim 5$都有，笔者自己的实验中，则取了$\alpha=4$，也没细调。至于Dropout的概率，跟笔者在《中文任务还是SOTA吗？我们给SimCSE补充了一些实验》所选的一样，设为0.3效果比较好。

论文报告 #

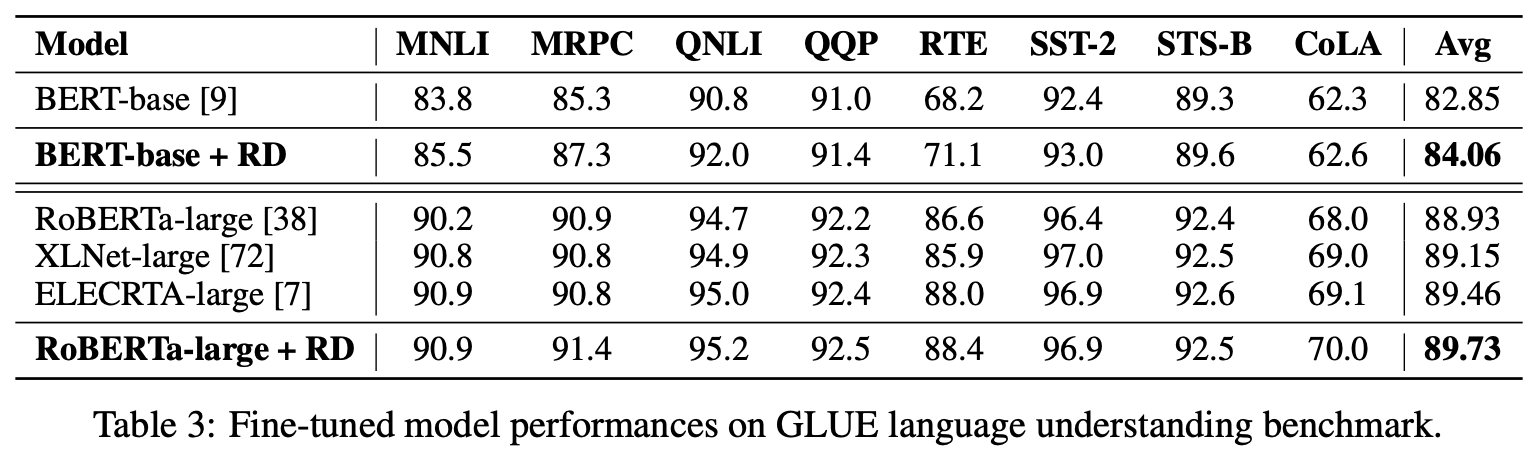
说实话，原论文所报告的R-Drop的效果是相当让人惊艳的，这也是笔者不得不要介绍一波R-Drop的主要原因。原论文在NLU、NLG、CV的分类等多种任务上都对R-Drop做了对比实验，大部分实验效果都称得上“明显提升”。

官方实现：https://github.com/dropreg/R-Drop

下面截图一部分实验结果：

R-Drop在机器翻译任务上的效果

R-Drop在GLUE任务上的效果

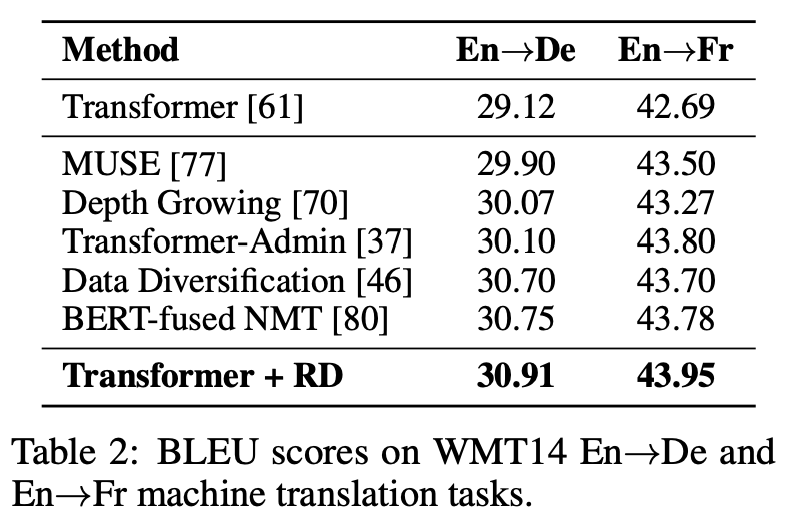
特别地，在机器翻译任务上，简单的“Transformer + R-Drop”超过了其他更加复杂方法的效果：

机器翻译任务上不同方法的对比

论文还包括自动摘要、语言模型、图像分类等实验，以及关于超参数的一些消融实验，大家仔细看原论文就好。总的来说，R-Drop的这份“成绩单”，确实足以让人为之点赞了。

个人尝试 #

当然，笔者坚持的观点是“没有在中文测试过的模型是没有灵魂的”，一般情况下笔者都是在中文任务上亲自尝试过之后，才会写作分享。

个人实现：https://github.com/bojone/r-drop

有中文监督任务上，笔者实验了两个文本分类任务（CLUE榜单的IFLYTEK和TNEWS）
\begin{array}{c|cc}
\hline
& \text{IFLYTEK} & \text{TNEWS} \\
\hline
\text{无对抗训练} & 60.29\% & 56.58\% \\
\text{加对抗训练} & 62.46\% & 57.66\% \\
\text{加梯度惩罚} & 62.31\% & \textbf{57.81%} \\
\text{加R-Drop} & \textbf{62.69%} & 57.51\% \\
\hline
\end{array}
和一个文本生成任务（CSL标题生成，参考《Seq2Seq中Exposure Bias现象的浅析与对策》）：
\begin{array}{c|cccc}
\hline
& \text{Rouge-L} & \text{Rouge-1} & \text{Rouge-2} & \text{BLEU} \\
\hline
\text{baseline} & 63.81 & 65.45 & 54.91 & 45.52 \\
\text{随机替换} & 64.44 & 66.09 & 55.56 & 46.1 \\
\text{梯度惩罚} & 65.41 & 67.29 & 56.64 & 47.37 \\
\text{R-Drop} & \textbf{65.51} & \textbf{67.41} & \textbf{57.12} & \textbf{47.82} \\
\hline
\end{array}
可以看到，R-Drop的结果足以PK在《对抗训练浅谈：意义、方法和思考（附Keras实现）》中介绍的著名正则化手段“对抗训练”和“梯度惩罚”了。

实现要点 #

相比于对抗学习等复杂正则化方法，R-Drop的实现难度可谓是相当低了，这里以bert4keras为例，简单介绍一下如何将一个普通的训练脚本改为带Dropout的模式。

首先，是数据生成部分，改动如下：

class data_generator(DataGenerator):
    """数据生成器
    """
    def __iter__(self, random=False):
        batch_token_ids, batch_segment_ids, batch_labels = [], [], []
        for is_end, (text, label) in self.sample(random):
            token_ids, segment_ids = tokenizer.encode(text, maxlen=maxlen)
            # batch_token_ids.append(token_ids)
            # batch_segment_ids.append(segment_ids)
            # batch_labels.append([label])
            for i in range(2):
                batch_token_ids.append(token_ids)
                batch_segment_ids.append(segment_ids)
                batch_labels.append([label])
            # if len(batch_token_ids) == self.batch_size or is_end:
            if len(batch_token_ids) == self.batch_size * 2 or is_end:
                batch_token_ids = sequence_padding(batch_token_ids)
                batch_segment_ids = sequence_padding(batch_segment_ids)
                batch_labels = sequence_padding(batch_labels)
                yield [batch_token_ids, batch_segment_ids], batch_labels
                batch_token_ids, batch_segment_ids, batch_labels = [], [], []

然后，自定义一个新loss：

from keras.losses import kullback_leibler_divergence as kld

def categorical_crossentropy_with_rdrop(y_true, y_pred):
    """配合上述生成器的R-Drop Loss
    其实loss_kl的除以4，是为了在数量上对齐公式描述结果。
    """
    loss_ce = K.categorical_crossentropy(y_true, y_pred)  # 原来的loss
    loss_kl = kld(y_pred[::2], y_pred[1::2]) + kld(y_pred[1::2], y_pred[::2])
    return K.mean(loss_ce) + K.mean(loss_kl) / 4 * alpha

最后把模型的Dropout打开，并用这个data_generator和categorical_crossentropy_with_rdrop来训练模型就行了。

个人理解 #

看完了让人赏心悦目的实验结果后，我们来啃一下理论。原论文提供了对R-Drop的一个理论分析，大致意思是R-Drop会促进参数的同化，从而起到正则化作用。不过个人感觉这个解释并不直观，而且还不够本质。下面笔者试图提供R-Drop的另外几个角度的理解。

一致性 #

R-Dropout可以看成是Dropout的改进，那Dropout有什么问题呢？其实Dropout是典型的训练和预测不一致的方法。具体来说，Dropout在训练阶段往（某些层的）输入加上了乘性噪声，使得模型从$f_{\theta}(x)$变成了$f_{\theta}(x,\varepsilon)$，其中$\varepsilon$的每个元素有$p$的概率为0，剩下$1-p$的概率为$1/(1-p)$，训练目标就是
\begin{equation}\mathbb{E}_{(x,y)\sim\mathcal{D}}\mathbb{E}_{\varepsilon}[l(y, f_{\theta}(x,\varepsilon))]\end{equation}
这样训练之后，我们应该用哪个模型预测最好呢？不确定，但如果损失函数是$l_2$距离的话，那么我们可以推出最佳预测模型应该是
\begin{equation}\mathbb{E}_{\varepsilon}[f_{\theta}(x,\varepsilon)]\end{equation}

推导：如果用$l_2$损失，此时单个样本的损失是
\begin{equation}\mathbb{E}_{\varepsilon}\left[\Vert y - f_{\theta}(x,\varepsilon)\Vert^2\right] = \Vert y\Vert^2 - 2\langle y,\mathbb{E}_{\varepsilon}\left[f_{\theta}(x,\varepsilon)\right]\rangle + \mathbb{E}_{\varepsilon}\left[\Vert f_{\theta}(x,\varepsilon)\Vert^2\right]\end{equation}
注意，现在我们的问题是“模型训练完后应该用什么函数来预测”，所以$f_{\theta}(x,\varepsilon)$是常数，$y$才是要优化的变量，这只不过是一个二次函数的最小值问题，容易解得$y=\mathbb{E}_{\varepsilon}[f_{\theta}(x,\varepsilon)]$时损失函数最小。

我们假定这个结果能泛化到一般情况。上式告诉我们，带Dropout的模型的正确步骤是“模型融合”：

对同一个输入多次传入模型中（模型不关闭Dropout），然后把多次的预测结果平均值作为最终的预测结果。

但我们一般情况下的预测方式显然不是这样的，而是直接关闭Dropout进行确定性的预测，这等价于预测模型由“模型平均”变成了“权重平均”：
\begin{equation}f_{\theta}(x,\mathbb{E}_{\varepsilon}[\varepsilon])=f_{\theta}(x,1)=f_{\theta}(x)\end{equation}
这里的$1$指的是全1向量。所以，我们训练的是不同Dropout的融合模型，预测的时候用的是关闭Dropout的单模型，两者未必等价，这就是Dropout的训练预测不一致问题。

现在，我们就不难理解R-Drop了，它通过增加一个正则项，来强化模型对Dropout的鲁棒性，使得不同的Dropout下模型的输出基本一致，因此能降低这种不一致性，促进“模型平均”与“权重平均”的相似性，从而使得简单关闭Dropout的效果等价于多Dropout模型融合的结果，提升模型最终性能。

连续性 #

本文开头就提到R-Drop与SimCSE的相似性，事实上它还跟另外一个方法相当相似，那便是“虚拟对抗训练（Virtual Adversarial Training，VAT）”。（不过R-Drop也没引VAT，难道就只有笔者觉得像吗？？）

关于VAT的介绍，大家可以参考笔者之前的文章《泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练》。简单来说，VAT也是通过一个正则项，使得模型对扰动更加鲁棒，增强模型本身的连续性（小的变化不至于对结果产生大的影响）。它们不同的地方在于加扰动的方式，VAT只把扰动加入到输入中，并且通过对抗的思想提升扰动的针对性；R-Drop的扰动则可以施加到模型的每一层中，并且扰动是随机的。

有读者可能想到了，VAT可是主打半监督训练的，那是不是意味着R-Drop也可以做半监督训练？这部分原论文并没有实验，是笔者自己做的实验，答案是确实可以，跟VAT类似，R-Drop新增的KL散度项是不需要标签的，因此可以无监督训练，混合起来就是半监督了，效果也还不错。下面是笔者的实验结果：
\begin{array}{c|cc}
\hline
& \text{验证集} & \text{测试集}\\
\hline
\text{非VAT} & 88.93\% & 89.34\%\\
\text{VAT} & 89.83\% & \textbf{90.37%}\\
\text{R-Drop} & \textbf{90.37%} & 90.14\%\\
\hline
\end{array}
可以看到，R-Drop的半监督效果完全不逊色于VAT，而且它实现比VAT简单，速度也比VAT快！看来VAT有望退休了～直觉上来看，虽然R-Drop的扰动是随机的，但是R-Drop的扰动更多，所以它造成的扰动也会放大，也可能比得上VAT经过对抗优化的扰动，所以R-Drop能够不逊色于VAT。

非目标类 #

一个比较直接的疑问是，如果我的模型够复杂，单靠交叉熵这一项，不能使得模型对Dropout鲁棒吗？KL散度那一项造成了什么直接的区别？

事实上，还真的不能。要注意的是，交叉熵的训练目标主要是：让目标类的得分大于非目标类的得分，这样模型就能正确地把目标类预测出来了（参考《将“Softmax+交叉熵”推广到多标签分类问题》）。也就是说，如果只有交叉熵这一项，模型的训练结果顶多是

不同的Dropout下，目标类的得分都大于非目标类的得分

而不能做到

不同的Dropout下，每个类的得分一致

所以也就没有解决训练预测不一致的问题。从公式上来看，交叉熵$\eqref{eq:ce}$只跟目标类别有关，不关心非目标类的分布，假如目标类为第一个类别，那么预测结果是$[0.5, 0.2, 0.3]$或$[0.5, 0.3, 0.2]$，对它来说都没区别。但对于KL散度项$\eqref{eq:kl}$来说就不一样了，每个类的得分都要参与计算，$[0.5, 0.2, 0.3]$或$[0.5, 0.3, 0.2]$是有非零损失的。

本文小结 #

本文介绍了R-Drop，它将“Dropout两次”的思想用到了有监督任务中，每个实验结果几乎都取得了明显的提升。此外，笔者在自己的实验还发现，它在半监督任务上也能有不俗的表现。最后，分享了笔者对R-Drop的三个角度的思考～

转载到请包括本文地址：https://www.spaces.ac.cn/archives/8496

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。