你的语言模型有没有“无法预测的词”？

众所周知，分类模型通常都是先得到编码向量，然后接一个Dense层预测每个类别的概率，而预测时则是输出概率最大的类别。但大家是否想过这样一种可能：训练好的分类模型可能存在“无法预测的类别”，即不管输入是什么，都不可能预测出某个类别$k$，类别$k$永远不可能成为概率最大的那个。

当然，这种情况一般只出现在类别数远远超过编码向量维度的场景，常规的分类问题很少这么极端的。然而，我们知道语言模型本质上也是一个分类模型，它的类别数也就是词表的总大小，往往是远超过向量维度的，那么我们的语言模型是否有“无法预测的词”？（只考虑Greedy解码）

是否存在 #

ACL2022的论文《Low-Rank Softmax Can Have Unargmaxable Classes in Theory but Rarely in Practice》首先探究了这个问题，正如其标题所言，答案是“理论上存在但实际出现概率很小”。

首先我们来看“理论上存在”。为了证明其存在性，我们只需要具体地构建一个例子。设各个类别向量分为$\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_n\in\mathbb{R}^d$，偏置项为$b_1,b_2,\cdots,b_n$，假设类别$k$是可预测的，那么就存在$\boldsymbol{z}\in\mathbb{R}^d$，同时满足
$$\begin{equation}\langle\boldsymbol{w}_k,\boldsymbol{z}\rangle + b_k > \langle\boldsymbol{w}_i,\boldsymbol{z}\rangle + b_i\quad (\forall i \neq k)\end{equation}$$
反过来，如果类别$k$不可预测，那么对于任意$\boldsymbol{z}\in\mathbb{R}^d$，必须存在某个$i\neq k$，满足
$$\begin{equation}\langle\boldsymbol{w}_k,\boldsymbol{z}\rangle + b_k \leq \langle\boldsymbol{w}_i,\boldsymbol{z}\rangle + b_i\end{equation}$$
由于现在我们只需要举例子，所以简单起见我们先考虑无偏置项的情况，并设$k=n$，此时条件为$\langle \boldsymbol{w}_i - \boldsymbol{w}_n, \boldsymbol{z}\rangle \geq 0$，也就是说，任意向量$\boldsymbol{z}$必然能找到向量$\boldsymbol{w}_i - \boldsymbol{w}_n$与之夹角小于等于90度。不难想象，当向量数大于空间维度、向量均匀分布在空间中时，这是有可能出现的，比如二维平面上的任意向量，就必然与$(0,1),(1,0),(0,-1),(-1,0)$之一的夹角小于90度，从而我们可以构造出例子：
$$\begin{equation}\left\{\begin{aligned} &\boldsymbol{w}_5 = (1, 1) \quad(\boldsymbol{w}_5\text{可以随便选})\\ &\boldsymbol{w}_1 = (1, 1) + (0, 1) = (1, 2)\\ &\boldsymbol{w}_2 = (1, 1) + (1, 0) = (2, 1)\\ &\boldsymbol{w}_3 = (1, 1) + (0, -1) = (1, 0)\\ &\boldsymbol{w}_4 = (1, 1) + (-1, 0) = (0, 1)\\ \end{aligned}\right.\end{equation}$$
在这个例子中，类别5就是不可预测的了，不信大家可以代入一些$\boldsymbol{z}$试试。

怎么判断 #

现在我们已经确认了“无法预测的类别”是可能存在的，那么一个很自然的问题就是，对于一个训练好的模型，也就是给定$\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_n\in\mathbb{R}^d$和$b_1,b_2,\cdots,b_n$，怎么判断其中是否存在不可预测的类别呢？

根据前一节的描述，从解不等式的角度来看，如果类别$k$是可预测的，那么下述不等式组的解集就会非空
$$\begin{equation}\langle\boldsymbol{w}_k - \boldsymbol{w}_i,\boldsymbol{z}\rangle + (b_k - b_i) > 0\quad (\forall i \neq k)\end{equation}$$
不失一般性，我们同样设$k=n$，并且记$\Delta\boldsymbol{w}_i = \boldsymbol{w}_n - \boldsymbol{w}_i, \Delta b_i = b_n - b_i$，留意到
$$\begin{equation}\langle\Delta\boldsymbol{w}_i,\boldsymbol{z}\rangle + \Delta b_i > 0\,(i = 1,2,\cdots,n-1)\quad\Leftrightarrow\quad \min_i \langle\Delta\boldsymbol{w}_i,\boldsymbol{z}\rangle + \Delta b_i > 0\end{equation}$$
所以，只要我们尽量最大化$\min\limits_i \langle\Delta\boldsymbol{w}_i,\boldsymbol{z}\rangle + \Delta b_i$，如果最终结果是正的，那么类别$n$就是可预测的，否则就是不可预测的。如果之前读过《多任务学习漫谈（二）：行梯度之事》的读者，就会发现该问题“似曾相识”，特别是如果没有偏置项的情况下，它跟多任务学习中寻找“帕累托最优”的过程是几乎一致的。

现在问题变为
$$\begin{equation}\max_{\boldsymbol{z}} \min_i \langle\Delta\boldsymbol{w}_i,\boldsymbol{z}\rangle + \Delta b_i\end{equation}$$
为了避免发散到无穷，我们可以加个约束$\Vert \boldsymbol{z}\Vert\leq r$：
$$\begin{equation}\max_{\Vert \boldsymbol{z}\Vert\leq r} \min_i \langle\Delta\boldsymbol{w}_i,\boldsymbol{z}\rangle + \Delta b_i \end{equation}$$
其中$r$是一个常数，只要$r$取得足够大，它就能跟实际情况足够吻合，因为神经网络的输出通常来说也是有界的。接下来的过程就跟《多任务学习漫谈（二）：行梯度之事》的几乎一样了，首先引入
$$\begin{equation}\mathbb{P}^{n-1} = \left\{(\alpha_1,\alpha_2,\cdots,\alpha_{n-1})\left|\alpha_1,\alpha_2,\cdots,\alpha_{n-1}\geq 0, \sum_i \alpha_i = 1\right.\right\}\end{equation}$$
那么问题变成
$$\begin{equation}\max_{\Vert \boldsymbol{z}\Vert\leq r} \min_{\alpha\in\mathbb{P}^{n-1}} \left\langle\sum_i \alpha_i \Delta\boldsymbol{w}_i,\boldsymbol{z}\right\rangle + \sum_i \alpha_i \Delta b_i\end{equation}$$
根据冯·诺依曼的Minimax定理，可以交换$\max$和$\min$的顺序
$$\begin{equation}\min_{\alpha\in\mathbb{P}^{n-1}} \max_{\Vert \boldsymbol{z}\Vert\leq r}\left\langle\sum_i \alpha_i \Delta\boldsymbol{w}_i,\boldsymbol{z}\right\rangle + \sum_i \alpha_i \Delta b_i\end{equation}$$
很显然，$\max$这一步在$\Vert\boldsymbol{z}\Vert=r$且$\boldsymbol{z}$跟$\sum\limits_i \alpha_i \Delta\boldsymbol{w}_i$同向时取到，结果为
$$\begin{equation}\min_{\alpha\in\mathbb{P}^{n-1}} r\left\Vert\sum_i \alpha_i \Delta\boldsymbol{w}_i\right\Vert + \sum_i \alpha_i \Delta b_i\end{equation}$$
当$r$足够大时，偏置项的影响就非常小了，所以这几乎就等价于没有偏置项的情形
$$\begin{equation}\min_{\alpha\in\mathbb{P}^{n-1}} \left\Vert\sum_i \alpha_i \Delta\boldsymbol{w}_i\right\Vert\end{equation}$$
最后的$\min$的求解过程已经在《多任务学习漫谈（二）：行梯度之事》中讨论过了，主要用到了Frank-Wolfe算法，不再重复。

（注：以上判别过程是笔者自己给出的，跟论文《Low-Rank Softmax Can Have Unargmaxable Classes in Theory but Rarely in Practice》中的方法并不相同。）

实践如何 #

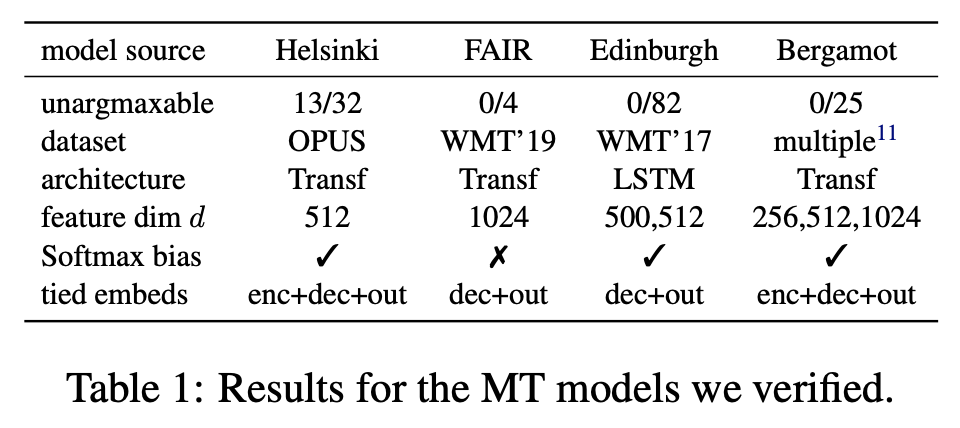
前面的讨论都是理论上的，那么实际的语言模型出现“无法预测的词”的概率大不大呢？原论文对一些训练好的语言模型和生成模型进行了检验，发现实际上出现的概率很小，比如下表中的机器翻译模型检验结果：

其实这不难理解，从前面的讨论中我们知道“无法预测的词”一般只出现在类别数远远大于向量维度的情况，也就是原论文标题中的“Low-Rank”。但由于“维度灾难”的原因，“远远大于”这个概念其实并非我们直观所想的那样，比如对于2维空间来说，类别数为4就可以称得上“远远大于”，但如果是200维空间，那么即便是类别数为40000也算不上“远远大于”。常见的语言模型向量维度基本上都有几百维，而词表顶多也就是数十万的级别，因此其实还是算不上“远远大于”，因此出现“无法预测的词”的概率就很小了。

另外，我们还可以证明，如果所有的$\boldsymbol{w}_i$互不相同但是模长都相等，那么是绝对不会出现“无法预测的词”，因此这种不可预测的情况只出现在$\boldsymbol{w}_i$模长差异较大的情况，而在当前主流的深度模型中，由于各种Normalization技术的应用，$\boldsymbol{w}_i$模长差异较大的情况很少出现了，这进一步降低了“无法预测的词”的出现概率了。

当然，还是文章开头说了，本文的“无法预测的词”指的是最大化预测，也就是Greedy Search，如果用Beam Search或者随机采样，那么即便存在“无法预测的词”，也依然是可能生成出来的。这个“无法预测的词”，更多是一个好玩但实用价值不大的理论概念了，

最后小结 #

本文向大家介绍了一个没什么实用价值但是颇为有意思的现象：你的语言模型可能存在一些“无法预测的词”，它永远不可能成为概率最大者。

转载到请包括本文地址：https://spaces.ac.cn/archives/9046

更详细的转载事宜请参考：《科学空间FAQ》