相对论、对称和第四维
By 苏剑林 | 2012-05-01 | 106287位读者 |这篇文章其实在年初就完成了。
众所周知,我们生活在一个平坦的世界中。正如我们能够感受到的那样,在这个被称为“欧几里得平直空间”的世界里,空间里两点间的最短曲线是两点间的直线段,空间里的任意直角三角形都满足勾股定理,每个物体都有着自己的长、宽、高,它们都随着时间的流逝而运动着。这种世界观把时间独立于空间之外,作为一个独特的研究对象。但是自爱因斯坦在1905年发表狭义相对论以来,我们的宇宙就被描述成为了由三维空间和一维时间组成的“四维时空”,在这里,时间和空间的地位是等价的。不少同好们也许会感到非常困惑:即使证明了时间与空间的确存在着某种联系,也不必要把时间描述成是世界的一维吧?在我们的感官里,时间明明就和空间的三维差别甚大,时间和空间怎么能够等同起来呢?其实答案很简单:为了美。把时间看成与空间等价的一维之后,整个力学体系体现出一种前所未有的对称美,这种美不仅让人赏心悦目,而且极大地方便了我们进一步处理问题。
对称
自然界似乎偏爱对称,如很多蝴蝶、蜻蜓、鸟类等外观都是对称的。我们中国中国自古就也对“对称”情有独钟,这可以从我们生活中各种对称的房屋、亭子等看到。不仅如此,它还出现在文人的作品之中,例如脍炙人口的牌匾“客上天然居,居然天上客”,还有清代女诗人吴绛雪的《春夏秋冬》中《秋》诗:
秋江楚雁宿沙洲,雁宿沙洲浅水流。流水浅洲沙宿雁,洲沙宿雁楚江秋。
正反读都一样,这无疑是一首绝妙的回文诗!
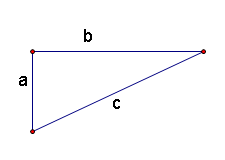
什么是对称呢?在我们的生活中,有很多对称的现象,诸如篮球的形状、人的体型、行星绕日的椭圆轨道,对称几乎无处不在。对称的概念是广泛的,我们上边举的是几何对称的例子,相应的还有代数对称。以直角三角形的勾股定理为例,我们知道,直角三角形的三边满足:
$$a^2+b^2=c^2$$
暂时忽略这个式子的几何意义,只把它看作一个普通的函数式,让我们把a、b交换位置,会得到什么呢?是
$$b^2+a^2=c^2$$
显然,这和原来的式子式等价的,那么我们就说,在式子$a^2+b^2$中,a、b的“地位”是等价的,$a^2+b^2$是一个对称式。对称的式子还有很多,诸如x+y、xyz、\sin(xy+yz+zx)等等,将这些式子的任意两个变量互换,式子并没有发生变化。在对称的式子,每个变量都具有同等的地位。
现在我们再来看$a^2+b^2=c^2$中的c变量,我们发现,将a与c互换之后,式子就会发生变化,显然,这里的a、c并非完全等价的。但要是我们将c移到左边,得到
$$a^2+b^2-c^2=0$$
利用复数的虚数单位i($i^2=-1$),式子就可以改写成
$$a^2+b^2+(ic)^2=0$$
这样在$a^2+b^2+(ic)^2$这个式子中,我们就使得a、b、ic处于完全等价的位置,而ic只不过是对c进行的一个线性变换,并没有改变性质,ic即是c。换言之,我们发现了c与a、b一种特殊的等效关系,在这种意义下我们应该“以同样的眼光”看待a、b、c。
也许有的同好会认为,这无非是数字游戏,既不能带来计算上的方便,又不符合直观感觉,何必如此大费周章呢?但读者是否想到过,当我们确立了a、b、c的同等地位后,每当我们发现了边a的相关规律时,可以毫不费力地将这个规律“改装”为边b、c的规律(既然地位是平等的,那么自然规律就不会偏爱某一边),而不必针对每边都重新推算一番,这无疑是省时省力的;另一方面,对称在很大程度上有助于我们揭示自然规律的内在奥妙。这大概就是对称的好处吧。
另一个物理学的例子就是达朗贝尔原理。我们都知道牛顿第二定律F=ma,达朗贝尔将其改写成F+(-ma)=0,并认为-ma也是一个力,于是所有力学系统都满足静力学平衡!一个看似简单的变换,实际向前迈进了一大步:用静力学原理来研究动力学,无疑会更方便深刻,因为静总比动容易控制。当然,笔者还仅仅处于涉猎的浅尝阶段,唯恐拙笔难以道出其中的美妙,所以这方面的描述就此搁笔了。
相对论中的对称
在被称为“奇迹年”的1905年,爱因斯坦发表了至今仍脍炙人口的狭义相对论,里边导出了洛伦兹变换(以一维空间为例):
$$\begin{aligned}x'=\gamma (x'-vt) \\ t'=\gamma (t-\frac{v}{c^2}x)\end{aligned}$$
在此不打算细说洛伦兹变换的推导(有兴趣的同好可以相关相对论书籍,维基百科也有相关内容),简单地说,这是一个物体在两个不同惯性系之间的坐标变换。我们都知道,不管选择什么坐标系,一个线段的长度都不会变化的,用数学可以写成$x^2+y^2+z^2= x'^2+y'^2+z'^2$。
细看洛伦兹变换,我们会发现下面的事实:
$x^2-c^2 t^2= x'^2-c^2 t'^2$。
这不禁让我们想到了勾股定理,我们将其改写成
$$x^2+(ict)^2= x'^2+(ict')^2$$
这样就和$x^2+y^2+z^2= x'^2+y'^2+z'^2$的形式一模一样了,而且每个量都具有长度的量纲!于是我们发现:时间和空间满足某种“距离”的不变性。对称意味着守恒,守恒意味着不变。这里我们找到了一个“不变量”,便意味着找到了一种对称。
现在重点来了。如前面所提到的,$x^2+(ict)^2$和$x'^2+(ict')^2$是一个对称的式子,这里的x与ict应当具有同等的地位,因此如果说x是时空的一维,那么ict应该也是时空的一维;而由t变成ict只是经过了一个线性的变换,因此(数学的)本质没有变化,所以时间t也属于时空的一维。狭义相对论提出后,很多人难以接受,因为它违反了很多经典物理直觉。但是闵可夫斯基的重新表述使得相对论不再是“违背常理”的坐标变换,而是一个具有统一、对称、简洁之美的时空理论,原来的三维空间中很多漂亮的结论都能够保持或简单推广。而且由于$x^2+(ict)^2= x'^2+(ict')^2$具有与勾股定理相同的形式,因此这实际狭义相对论变成了一个几何理论!从此,世界多出了一维。
不过,空间与时间可以组成一个四维时空,但是时间与空间只是在数学上具有等价性,但是在物理上不完全等价,如时间并没有像空间一般可以自由移动的特性,因此这里的“时空”,是数学上的“空间”而非物理上的“空间”。
科学巨匠的传奇人生
以上将狭义相对论几何化是爱因斯坦的老师赫尔曼?闵可夫斯基(德语:Hermann Minkowski,1864年6月22日-1909年1月12日)的首创。
闵可夫斯基说:“爱因斯坦在学生时期是条懒狗。他一点也不为数学操心。”爱因斯坦的狭义相对论的确使闵可夫斯基大吃一惊,但是,真正认识到狭义相对论价值并且从哲学和数学上推进一大步的也正是闵可夫斯基。
赫尔曼·闵可夫斯基出生于俄国,他是三兄弟中最小的。有趣的是,他的家庭无疑极度成功:父亲是一个成功的犹太商人;大哥继承父业也成为优秀的商人;二哥就是被称为“胰岛素之父”的奥斯卡·闵可夫斯基(Oscar Minkowski);后来他的侄子鲁道夫也成为美国著名的天文学家。而赫尔曼·闵可夫斯基少年时期就因为极高的数学天赋被称为神童。当时闵可夫斯基兄弟三人声名显赫。
1873年闵可夫斯基(以下的“闵可夫斯基”都指赫尔曼?闵可夫斯基)进入艾尔斯塔特预科学校读书,只用了五年半时间就完成了八年的学业。毕业后他先进入当地的大学,而后转入柏林大学,不久之后又回到哥尼斯堡大学。大学期间他曾师从亥姆霍兹、克罗内克、维尔斯特拉斯、基尔霍夫等数学家。在哥尼斯堡大学,闵可夫斯基和旧时好友希尔伯特(Hilbert)相遇,结为挚友。
这里边还有一段有趣的故事。1884年,年方25的数学家霍尔维茨(Hurwitz)来到哥尼斯堡大学当副教授,出于共同的爱好,他和闵可夫斯基及Hilbert建立起了深厚的友谊。每天下午五点,他们三人在苹果园里散步,讨论当前的数学问题,时而低头苦思、时而滔滔不绝,时而争辩,时而会心地哈哈大笑,旁人看来如同一群数学疯子。然而,这些讨论对数理界产生了重要的影响。希尔伯特后来写道:“在无数次的散步中,我们三人探究了数学科学的每一个角落。霍尔维茨学识渊博,他总是我们的带路人。”
大学期间,闵可夫斯基就曾因出色的数学工作而获奖。1895年他接替希尔伯特担任哥尼斯堡大学教授,第二年转到瑞士苏黎世联邦理工学院工作。这期间,青年时期的爱因斯坦在该校求学,成为闵可夫斯基的学生。两个科学界天才巨匠相遇,他们就在这里碰撞出璀璨的科学焰火!
1902年,闵可夫斯基受克莱因的邀请,转入哥廷根大学担任数学教授。1905年以后,闵可夫斯基将几乎所有精力放在电动力学上。1907年,闵可夫斯基认识到可以用非欧空间来描述洛伦兹和爱因斯坦的工作,将过去被认为是独立的时间和空间结合到一个四维的时空结构中,即闵可夫斯基时空。闵可夫斯基时空为广义相对论的建立提供了框架。1908年在德国科隆的一次演讲中,闵可夫斯基提出了四维时空的概念。
据此,同一现象的不同描述能用简单的数学方式表出。这些工作为狭义相对论提供了骨架。诺贝尔物理奖得主M. Bonn 曾说,他在闵可夫斯基的数学工作找到了“相对论的整个武器库”。
1909年1月10日,闵可夫斯基突患急性阑尾炎,抢救无效(据说原因是麻醉失败),于1月12日去世,去世时年仅45岁。一代天才居然就这样无辜地陨落了,不得不说是科学界的一大损失。为纪念他,科学界把第12493号小行星命名为“闵可夫斯基”。
几何化背后的秘密:美的追求
为什么要将物理理论几何化,难道物理理论比不上数学?一开始爱因斯坦看到他的老师的文章时也对其不以为然,觉得不会带来任何好处。但后来他发现只有将相对论高度几何化,才能够构建出普适于一切参考系、包含引力在内的广义相对论,所以他开始重视他老师的结果,给予高度评价,并向他的同学请教有关黎曼几何与张量分析。
原来,为了满足我们对美的追求,物理定律应该要符合一些对称的法则,而对称起源于几何,所以需要用几何来描述物理,而且由于几何理论在成熟性,这也给我们在处理物理问题或构思新理论时,提供了更加强有力的工具;另一方面,几何是用对称来描述的,一个几何化的物理世界便意味着一个对称、和谐、美的世界,这更让我们惊叹造物主的神奇!还有,这其实也是一个哲学的思考:谁知道物理世界不是一个几何世界呢?或许世界本来就是这样?
可惜,那时闵可夫斯基已经去世了,无法看到他的理论在爱徒的创造下大放光彩。
转载到请包括本文地址:https://www.spaces.ac.cn/archives/1602
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (May. 01, 2012). 《相对论、对称和第四维 》[Blog post]. Retrieved from https://www.spaces.ac.cn/archives/1602
@online{kexuefm-1602,
title={相对论、对称和第四维},
author={苏剑林},
year={2012},
month={May},
url={\url{https://www.spaces.ac.cn/archives/1602}},
}












May 2nd, 2012
嗯哪,你的观点的确让人眼前一亮!写完狭义相对论可以写写广义相对论啊,期待新大作!!嘿嘿
谢谢!广义相对论就比较困难了,我目前的物理数学水平还很低。^_^
你谦虚啦,按你的逻辑缜密程度来看,你的高数早就不在话下了,比我不知好多少倍,我刚才看了下我复变函数的成绩,才73,,看到我几乎虚脱,,来大学这么久了,得甘低分还是第一次,,离高考越来越近啦,应该胸有成竹了吧?加油噢!^^
没有谦虚,高等数学是多么精深,我怎么可能这么快就能够学好呢?就好像复变函数,对于我来说只是一个概念,什么都不会。即使对于高考,我也不能说很有把握,成绩波动比较大。你也要加油!
高数对你来说并不是精深不精深啦,只学早学迟而已,闻道有先后嘛。我所说的逻辑缜密度是说处理问题时考虑的周全不周全,解决问题有没有效,这方面,看得出你作得很好。你可是参加过国际性的大考试啊,高考怕个啥?好好复习,看总结性的东西和典型例子可能会好点噢。我也想学你一样写写文章了,互相学习哈~^^
May 3rd, 2012
域名有些牛X!
May 13th, 2012
那个将时间看作空间的一维的变换我在书上看过,不知你是自己思考出来的吗?
具体细节可以说是我自己想出来的,但是整体观念当然是前人的成果啦。我只是从一个很小的角度弄清楚(或者说根本就没有弄清楚)了“怎么把时间看做一维”而已。
May 13th, 2012
话说也快高考了,考完我也准备重操旧业,研究研究
May 20th, 2012
欧几里得
--
欧几里德
April 4th, 2013
能否发个帖子讲讲拉普拉斯变换啊?我觉得这个东西很神秘,人家怎么会那么想,怎么会有这种变换。
感谢你的建议,很遗憾,我对拉普拉斯变换也只是略懂皮毛。
一开始我看到这个变换的时候,也感到非常神奇,但是后来就发现,它仅仅是一个线性微分方程的工具,印象中当初感觉有点失望。
但是现在看来,这个变换产生于那个年代,是相当了不起了。我确实还没有弄清楚怎么才可以“比较自然地”得到这个变换的思想。
还需要多研究一下,有结果了会和大家分享的。
用幂函数展开
F(x)=∑∞ a_n x^n
可以联想到
F(x)=∫0 ∞ a(t) x^t dt
令x^t=(e^(Inx))^t,记-s=-Inx
F(x)=∫0 ∞ a(t) e^(-st) dt
Done
要研究的可逆性问题。怎么说呢?一般的《数学物理方法》是先研究傅里叶变换再研究拉普拉斯变换的,如果直接着手拉普拉斯变换,会涉及到狄拉克函数$\delta(x)$的。
我也不知道怎么才有一个比较自然的思路得出它?
April 10th, 2013
实质就是“长度”的定义(度量)决定的……固有时……
但是,1.为什么t非得是一维,不能是多维?
2.觉得爱因斯坦有拼凑的成分……(个人觉得,爱因斯坦的思想是:能量、动量守恒,因此其协变导数为0,如果时空的“曲率”是由引力引起的,那么也应该“找”一个与曲率有关的量,能让它的协变导数也为0)
3.在奇点失效
现在还在学习这方面的内容,不便过早评价太多^_^过一段时间再和大家探讨这个问题。
December 12th, 2019
“那么$ict$应该也是时间的一维;”应该把时间改成时空吧……
已更正^_^
February 25th, 2022
广义相对论中就是以(1,1,1,i)为基建立时刻坐标的。不过虚单位i的存在恰恰说明时间与空间不对称。不过我有个想法,如果每个时空维度能来个解析拖延,全变成复数坐标,时空就真的对称了。到时候问题就是空间的虚轴有什么物理意义,时间的实轴呢?
February 25th, 2022
楼上看过书么?时空是一个二元组 $(M, g_{αβ})$,其中 M 是一个 4-维的微分流形(Hausdorff、连通),而 $g_{αβ}$ 是时空上的度规,它的号差为 (−1, 1, 1, 1);简言之,广义相对论中的时空是一个 4-维的 Lorentz 流形,相对论性时空只引入一个度规,是不先验地区分时间和空间的。
楼上的意思是为啥度规的时间分量是-1而其余是正1~
Minkowski度规约定?只要有空-时间隔不变性就可以推出来的,至于ict这样的度规约定,是用在wick转动上的。至于东西海岸度规约定,可以分辨出对方是搞粒子物理的 还是弦论或宇宙学的。