关于维度公式“n > 8.33 log N”的可用性分析
By 苏剑林 | 2021-09-27 | 56982位读者 |在之前的文章《最小熵原理(六):词向量的维度应该怎么选择?》中,我们基于最小熵思想推导出了一个词向量维度公式“$n > 8.33\log N$”,然后在《让人惊叹的Johnson-Lindenstrauss引理:应用篇》中我们进一步指出,该结果与JL引理所给出的$\mathcal{O}(\log N)$是吻合的。
既然理论上看上去很完美,那么自然就有读者发问了:实验结果如何呢?8.33这个系数是最优的吗?本文就对此问题的相关内容做一个简单汇总。
词向量 #
首先,我们可以直接,当$N$为10万时,$8.33\log N\approx 96$,当$N$为500万时,$8.33\log N\approx 128$。这说明,至少在数量级上,该公式给出的结果是很符合我们实际所用维度的,因为在词向量时代,我们自行训练的词向量维度也就是100维左右。可能有读者会质疑,目前开源的词向量多数是300维的,像BERT的Embedding层都达到了768维,这不是明显偏离了你的结果了?
事实上,像FastText之类的开源词向量是300维,也没法否定128维能够达到类似效果的可能性。至于BERT,它本身并不是一个词向量模型,所以它选多少维跟词向量维度的选择也没有直接关系,何况ALBERT已经表明,将Embedding层进行低秩分解(降到128维)几乎不会改变模型效果,因此BERT的768维Embedding多多少少是有冗余的。
关于词向量的评价,2015年有一篇比较全面的论文《How to Generate a Good Word Embedding?》可以参考,文中显示其实词向量在超过50维之后的提升就比较弱了,这也算是$n > 8.33\log N$的一个佐证吧~
注意力 #
公式$n > 8.33\log N$的另一个间接的实验证明来自注意力机制。在《让人惊叹的Johnson-Lindenstrauss引理:应用篇》我们分析过,Attention矩阵的计算公式跟词向量的Skip Gram模型是数学等价的,这就意味着$n > 8.33\log N$这个公式同样可以用于注意力机制的head_size选择问题。
在注意力机制中,$N$就是要处理的序列长度,常见的预训练长度是512,代入后得到$8.33\log 512\approx 52$,这与当前主流的head_size大小$64$非常接近,因此这间接证明了$n > 8.33\log N$的可用性。反过来,如果承认这个公式,那么这就解释了注意力机制的head_size为什么只需要64,也间接解释了注意力机制为什么要多个小的head而不是一个大的head的问题。
关于注意力机制的head_size选择与表达能力问题,还可以参考《On the Expressive Power of Self-Attention Matrices》。
图网络 #
如果将每个词看成一个节点,将词与词之间的共现看成边,那么Skip Gram也可以视为一个简单的图模型,所以,关于词向量维度的选择结果,理论上也可以用于图网络的嵌入维度选择。
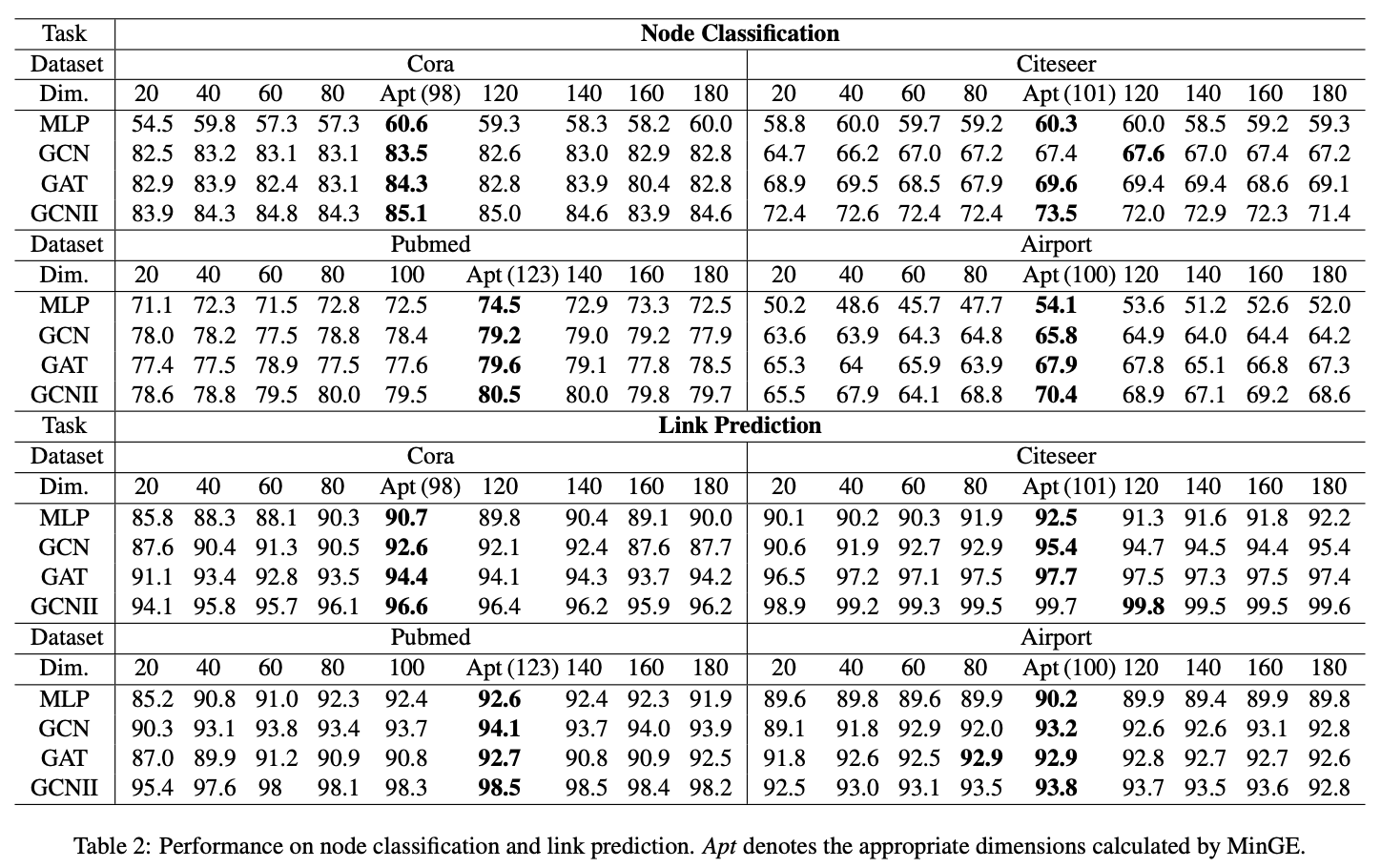
这方面的结果可以参考论文《Graph Entropy Guided Node Embedding Dimension Selection for Graph Neural Networks》,文中同时考虑了图的特征熵和结构熵,其中特征熵跟Skip Gram类似,采用了跟《最小熵原理(六):词向量的维度应该怎么选择?》同样的近似,所以这部分本质上也是公式$n > 8.33\log N$。
将特征熵和结构熵结合后,用它计算出来的结果作为图网络的嵌入维度来进行各种图任务,实验结果显示该方法确实能得到较优的维度选择结果:
小总结 #
本文对之前导出的维度选择公式$n > 8.33\log N$的可用性进行了分析,综合了词向量、注意力、图网络的已有的一些实验结果,显示出该公式可以得到比较合理的维度估计结果,通过也表明通过熵来进一步确定JL引理中$\log N$的常数也许是一个可行的选择。
转载到请包括本文地址:https://www.spaces.ac.cn/archives/8711
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Sep. 27, 2021). 《关于维度公式“n > 8.33 log N”的可用性分析 》[Blog post]. Retrieved from https://www.spaces.ac.cn/archives/8711
@online{kexuefm-8711,
title={关于维度公式“n > 8.33 log N”的可用性分析},
author={苏剑林},
year={2021},
month={Sep},
url={\url{https://www.spaces.ac.cn/archives/8711}},
}










April 4th, 2022
词嵌入是将向量从高维稀疏映射到低维稠密向量,我用的训练集里的单词种类只有18种,请问设置的词向量维度可以比18大吗?
可以肯定是可以的。
但这样不会违背词嵌入定义吗?就不是高维嵌入到低维了
没有必须说一定是高维嵌入低维才叫词嵌入吧?只是一般情况下满足这个条件而已。
June 1st, 2023
[...]维度选择公式:n>8.33logNJL理论:塞下N个向量,只需要
February 28th, 2025
[...]ALBERT: A Lite BERT for Self-supervised Learning of Language Representations[C]// International Conference on Learning Representations Distributed Representations of Words and Phrases and their Compos[...]
October 3rd, 2025
“将Embedding层进行低秩分解几乎不会改变模型效果”,这个结论有可能反过来用吗?比如我在一个小的模型上训练一些特殊的token(prefix tuning),然后对这些token做一些轻量级的调整后,直接拿到更大的大模型上用
你这个目标应用,假设并不是“Embedding层进行低秩分解几乎不会改变模型效果”,而是“大模型与小模型的Embedding层几乎是同构的”,后者需要更仔细地验证是否成立。
感谢苏神回复,我后来也发现这个假设有点问题,因为prefix tuning得到的这个向量除了在维度上和embedding是一样的之外,其实和embedding层没有任何关系,而是和整个模型的参数有关,还是得做实验看看有没有相似性。