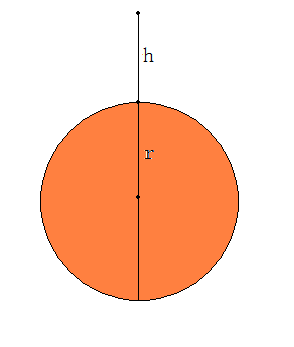
自由落体公式-示意图

自由落体公式-示意图

自由落体的一般定义是：只考虑吸引天体和被吸引天体的引力因素，忽略其他的运动和大气摩擦等因素，物体从静止（相对于吸引天体）开始接近吸引天体的运动。根据这个定义，假设地球为一个均匀球体，半径为r，质量为M，物体从距离地表h高度处自由落下。求落到地面的时间t，或者根据时间t求h。

令s为t时刻物体左右下落的物体与地表的距离，忽略物体的小质量，那么可以列出微分方程：
$$\frac{d^2 s}{dt^2}=-\frac{GM}{(r+s)^2}\tag{1}$$并且初始条件是$t=0,s=h,\dot{s}=v=0$

在实际应用中，我们不必求出这道微分方程的精确解，因为这个解极其麻烦，在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。根据泰勒级数展开式
$$f(x)=f(x_0)+f'(x_0)(x-x_0)+f''(x_0)\frac{x^2}{2!}+f'''(x_0)\frac{x^3}{3!}+...$$

对于上述的微分方程(1)，我们已经有了$s(0)=h,s'(0)=0,s''(0)=-\frac{GM}{(r+h)^2}$，由于$\frac{d\ddot{s}}{dt}=\dot{s}\frac{d\ddot{s}}{ds}$，并且不难证明$\frac{d\ddot{s}}{ds}$是有限的，所以$s'''(0)=0$，于是我们可以写出微分方程的近似解：
$$s=h-\frac{GM}{2(r+h)^2}t^2\tag{2}$$
它的截断误差是$O(t^4)$。如果求落到地表所用时间，那么有s=0，则
$$h=\frac{GM}{2(r+h)^2}t^2\tag{3}$$
另外，我们还有$GM=r^2 g$，g是地球表面的重力加速度。于是(3)又可以改写成
$$h=\frac{r^2 g}{2(r+h)^2}t^2\tag{4}$$
上述精确度有多高？我们不妨从h很小和h很大两方面来验证：

首先对于h远远小于r的情况，我们有$\frac{r^2}{(r+h)^2}\approx 1$，于是(4)退化成
$$h=\frac{g}{2}t^2\tag{5}$$这正是我们在高中接触到的自由落体的公式！

其次是对于r远远小于h的情况，我们不妨用这条公式求一下之前的一道题目：

一个物体自由下落， 9天后到达地面，问这个物体刚开始下落时的高度。

由于r远远小于h，得到：
$$h(r+h)^2=\frac{r^2 g}{2}t^2 \approx h^3\tag{6}$$
我们把$r=6371000m,t=9*86400s,g=9.8m//s^2$代入(6)，可以计算得到：
$h=515482465m=51.5*10^4 km$，这与官方答案几乎完全相等！

由此可见，修正后的自由落体公式具有很高的正确性！因此，参加天文奥赛的朋友不妨掌握这公式，或者评卷人还会给大家额外的加分呢！（创意分^_^）

转载到请包括本文地址：https://spaces.ac.cn/archives/584

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Apr. 04, 2010). 《关于自由落体公式的简单修正 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/584

@online{kexuefm-584,
        title={关于自由落体公式的简单修正},
        author={苏剑林},
        year={2010},
        month={Apr},
        url={\url{https://spaces.ac.cn/archives/584}},
}